Дисперсия

Рассмотрим меру вариации/рассеяния/разброса/изменчивости для метрической шкалы. По эмпирической кривой распределения или гистограмме на рис. 3.2.3 видим, что совокупность студентов неоднородна по продолжительности затрат времени на учебу. С одной стороны, очевидно, что средняя продолжительность учебы как ха­рактеристика имеет смысл, поскольку вполне правомерно сравне­ние средней продолжительности учебы для выделенных нами групп студентов: социологов, политологов, культурологов и т. д. С другой стороны, в ситуации неоднородности такое сравнение содержательно ни о чем не говорит.

Какова может быть мера неоднородности/однородности по продолжительности? Об этом можно судить по степени отклонения продолжительности затрат времени на учебу отдельного студента от сред­ней продолжительности, которая в нашем случае равна 5,7 (в часах). Индивидуальные отклонения (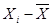)нельзя просто суммировать, чтобы судить об общем отклонении. Отклонения в одну сторону бу­дут погашаться отклонениями в другую. Чтобы этого не было, инди­видуальные отклонения возводятся в квадрат, а затем складываются. Эта сумма делится на число респондентов, и получается характерис­тика, называемая дисперсией (s²). Это мера вариации значений признака в среднем и вокруг средней арифметической.

s²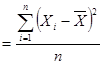

Следует заметить, что при небольшом числе объектов делить нужно не на n, а на (n ¾1). Для социолога это не принципиально, так как он работает обычно с достаточно большим числом объектов.

Корень квадратный из дисперсии называется среднеквадратическим отклонением ( s ¾ сигма). По ней можно сравнивать меры рассеяния разных признаков, одного признака для различных сово­купностей. Прямое сравнение дисперсий, среднеквадратических отклонений мало что дает. Рассмотрим пример из нашего исследо­вания. Вычислим среднее арифметическое и среднеквадратическое отклонение продолжительности затрат времени на учебу для нескольких групп студентов. Допустим, что для социологов (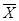 = 6, s = 4), психологов ( 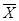= 5,4, s =3,5), политологов ( 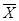= 4,5, s = 3,5), историков ( 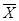= 6, s = 2). Какие выводы можно сделать по этим данным?

Социологи и историки затрачивают на учебу в среднем одина­ковое время, но совокупность социологов менее однородна, потому что среднеквадратическое отклонение больше. Психологи затрачи­вают на учебу в среднем больше времени, чем политологи, и они более однородны, чем группа политологов. Дисперсия одинакова в этих группах, относительно разных по значению средних. Когда средние и дисперсии в сравниваемых группах различны, на помощь приходит коэффициент вариации.

Коэффициент вариации

Этот коэффициент при наших обозначениях равен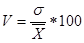

Он представляет собой долю вариации в процентах (%), приходящуюся на единицу средней. В нашем случае соответ­ственно четырем группам: V₁ = 66,7% (для социологов), V₂ = 64,8% (для психологов), V₃ = 77,8% (для политологов), V₄ = 33,3% (для историков). Таким образом, группа историков более однородна по продолжительности затрат времени на учебу, чем все осталь­ные группы. Самая неоднородная группа ¾ политологи. Это означает, что среди них оказались и очень много, и очень мало занимающиеся.

Среднее арифметическое и дисперсия интерпретируются всегда вместе. Например, существует так называемое правило «трех сигм», очень важное при работе с эмпирией. Оно означает, что если все значения признака находятся в интервале от -З s до +3 s, то счи­тается, что закон распределения признака нормальный, т. е., как минимум, эмпирическая кривая имеет унимодальный характер (одна мода, один горб). На рис. 3.2.5 изображен идеальный нормальный закон распределения. Запомните его, ибо математический аппарат для анализа нормальных распределений очень богат. Для идеально нормального распределения мода, медиана и среднее арифметичес­кое равны.

Если для анализа распределений использовать «язык» статистического анализа, то сами рассмотренные характеристики, например 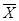, являются величинами, имеющими свой собственный закон распре­деления. Представим себе, что каждый из вас для одного и того же исследования сформировал выборочную совокупность. Пусть у каждо­го будет самая из самых «хорошая» (репрезентативная) выборка. Если подсчитать, к примеру, средний возраст опрошенных по этим выбор­кам, то значения будут различны. Среднее этих значений и будет ис­тинным значением среднего возраста в генеральной совокупности. Ана­логичны рассуждения и в случае средней продолжительности затрат времени на учебу.

Отклонение средних от «истинной средней» будет носить слу­чайный характер. Оказывается, эту случайность можно оценить. На этом основан подсчет так называемых доверительных интервалов, т. е. интервалов, в которых находится истинное (для генеральной совокупности) значение признака. Но это только для тех величин (характеристик), для которых известен закон распределения. Они называются статистиками. Среднее арифметическое и является ста­тистикой с нормальным законом распределения. Для нее легко оп­ределяется доверительный интервал.

Другие меры вариации

Рассмотрим меру вариации, меру отклонения, меру рассеяния значений признака вокруг медианы. Такой мерой является квартильный размах, с которым мы встречались при построении шка­лы Л. Терстоуна. Вспомним, что содержательно это интервал, в котором вокруг медианы сосредоточилось 50% экспертов. Это един­ственная мера вариации для порядковых шкал. На рис. 3.2.4 три пунктирные линии проведены для определения медианы и соот­ветствующего ей квартильного размаха {он равен }. Без сравнительного контекста трудно сказать, мало это или много. Для социолога познавательная возможность любого математичес­кого конструкта, а это пока простейшие формулы на уровне обы­денного понимания, определяются только в сравнительном кон­тексте, т. е. при сравнении значений, полученных в разных условиях.

Перейдем к самым трудным для понимания мерам ¾ мерам качественной вариации, т. е. мерам вариации для признаков, изме­ренных по номинальным шкалам. Самое главное, что любая такая мера характеризует степень отклонения распределения признака от равномерного, т. е. когда каждой градации признака соответствует одно и то же число объектов. Максимальное значение меры обыч­но соответствует ситуации равномерного распределения, а мини­мальное ¾ ситуации, когда все объекты сосредоточены в одной гра­дации.

Как мы знаем, любой номинальный признак сводится к сово­купности бинарных, дихотомических, т. е. принимающих значе­ния 0 или 1. В этом случае столбец нашей исходной матрицы дан­ных «объект-признак», соответствующий одному признаку, превращается как бы в несколько столбцов, каждый из которых соответствует отдельному свойству (быть социологом, быть поли­тологом и т. д.). Анализировать мы должны теперь поведение «свой­ства», а не признака. По всем объектам это совокупность из нулей и единиц.

0000 1 1 1 1 1 1...00 1 1 1

Предположим, что этот ряд получен по свойству ¾ быть в буду­щем социологом. Если i-й студент ¾ социолог, то ему соответствует х_i =1, а если он не социолог, то х_i = 0. Оказывается, для такого вида данных имеет смысл среднее арифметическое. Она равна 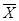= k/n, где k ¾ число будущих социологов, a n ¾ число всех студентов-гума­нитариев.

Почему имеет смысл средняя арифметическая для дихотоми­ческой шкалы? Потому что она содержательно интерпретируется. Если 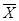= 0, то это означает, что все студенты-гуманитарии в нашей выборке не социологи. Если 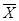= l, то все студенты ¾ социологи. Если 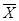= 0,5, то половина студентов 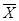будущие социологи, а половина ¾ не социологи. Продолжая наши рассуждения, можно сде­лать вывод и для случаев,_когда 0 < 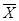< 0,5 и 0,5 < 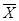< 1. Первый из них означает, что в совокупности меньше 50% студентов социологи. Второй ¾ в сово­купности больше 50% социологов.

Таким образом, как это ни парадоксально, можно вычислять среднее арифметическое по признаку «пол». Только важно пра­вильно интерпретировать полученный результат, исходя из того, каким образом закодирован этот признак. Разумеется, социологу нет никакого смысла в использовании такого рода средней, отра­жающей «центральную тенденцию». Он прекрасно работает с от­носительными частотами в %. Приведенная средняя интересна не для целей первичного анализа, а для анализа с применением слож­ных математических методов. К примеру, для такой средней можно подсчитать дисперсию. Если для дихотомических признаков имеет смысл использование характеристик метрической шкалы, значит, возможно использование и математических методов, работающих с метрическими данными. Дисперсия в данном случае равна:

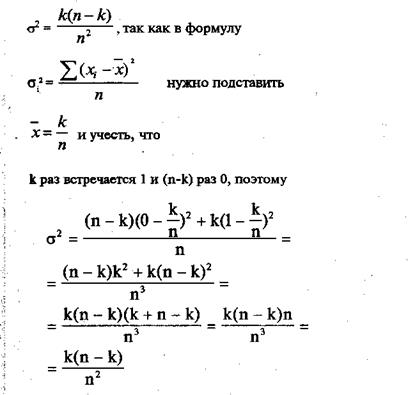
Эта дисперсия и является мерой вариации для бинарного (дихотомического) признака. При этом она равна нулю, если все объекты либо обладают, либо не обладают анализируемым свойством. Что естественно, так как вэтих случаях разброса в данных не наблюда­ется. Максимальное значение этой дисперсии достигается в случае равномерного распределения (k = n/2), и оно равно 1/4. При этом 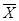= 1/2, s= 1/2, V=100%.

Напомню вам одно правило из школьной арифметики. Если есть два целых числа, то среднее геометрическое этих чисел всегда меньше или равно среднему арифметическому. Равенство достига­ется, когда числа равны.

Этим соотношением и воспользуемся для введения коэффици­ента качественной вариации. Вначале предположим, что номиналь­ный признак имеет только две градации, причем в первую града­цию попало N₁ объектов, а во вторую ¾ N₂ объектов {число всех объектов равно n = N₁ + N₂,). И если теперь в соотношение между средней арифметической и средней геометрической подставить

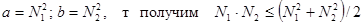
Максимальное значение N, • N₂ будет только в случае N₁ = N₂, и оно будет равно _п² / 4. А это ведь случай равномерного распре­деления. Коэффициентом качественной вариации и будет отноше­ние реального значения произведения (N, • N₂) к максимальному его значению, равному п² / 4.

Коэффициент равен нулю, если все объекты в одной градации, и единице, если распределение равномерное. Коэффициент легко обобщается на случай, когда число градаций равно k. Представим себе, что из всей совокупности объектов мы образовали всевозмож­ные пары. Вспомним метод парных сравнений Терстоуна и вычис­ление числа всевозможных пар для сравнения объектов. Здесь ситу­ация аналогичная. Пары не повторяются, объект сам с собой пару не образует. В случае двух градаций произведение (N₁ • N₂) есть не что иное, как число пар, различных между собой.

Если градаций три и по ним частоты равны (N₁, N₂, N₃), то число различных пар будет равно (N₁×N₂ + N₁×N₃ + N₂×N₃). Число членов в этой сумме вычисляется как число парных сочетаний из трех элементов по два. Вспоминаем, что это число равно k(k-l)/2, когда число элементов равно k.

Тогда коэффициент вариации вычисляется как отношение:

реального числа различных пар, равного (N₁×N₂ + N₁×N₃ + N₂×N₃);

к максимальному (случай равномерного распределения), равному {(n² / 9)(3 • 2 / 2)}. В первых круглых скобках ¾ то, во что превращается каждый член суммы, а во вторых ¾ число членов в этой сумме.

В общем случае для k градаций реальное число пар равно

. Таким образом, формула для вычисления коэффициента качественной вариации приведена по частям, т. е. отдельно числитель (реаль­ное) и отдельно знаменатель (максимальное).

Коэффициентом вариации (R) может служить и величина, рав­ная среднему геометрическому из относительных частот в долях (ча­стости) умноженному на число градаций, т. е.

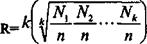
Для вычисления этой величины необходимо избавиться от пус­тых градаций, иначе она обратится в нуль. R=l при равномерном распределении.

Приведем еще один пример вычисления меры качественной вариации. В качестве такой меры служит энтропия, о которой мы упоминали в контексте «языка» анализа распределений, опираю­щегося на информационный подход. Энтропия ¾ это основное по­нятие так называемой теории информации. Распределение призна­ка интерпретируется как некое сообщение, несущее определенный объем информации. Этот объем можно оценить энтропией как ме­рой «определенности»/«неопределенности». Ее трудно объяснить и трудно понять без знания логарифмов и логарифмических законов распределения. Более того, замечательные свойства этой меры мо­гут быть оценены только при многомерном анализе. Пока вам при­дется просто этому поверить. Итак, энтропия Н(х) при числе града­ций равном k и при обозначении i-й частости (доли) через р_; равна:

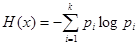
Логарифм может быть взят по любому основанию, ибо нетруд­но перейти от одного основания к другому. Напомним, что есть натуральный логарифм (по основанию «е»), десятичный (по осно­ванию «10»), двоичный (по основанию «2»).

Энтропия ¾ положительная величина, несмотря на то, что перед суммой стоит минус. Он погашается другим минусом, появляю­щимся за счет того, что логарифм берется от правильной дроби (это вам известно из школьной математики). Значение энтропии равно нулю, если все объекты сосредоточены в одной градации (но чтобы это показать, нужны знания о «пределах» ¾ lim). В самом деле, тогда мера неопределенности минимальная. Энтропия равна log k, если распределение равномерное, т. е. в этом случае максимальная неопределенность. Чтобы значение меры не зависело от числа гра­даций, можно использовать в качестве меры качественной вариа­ции нормированную величину энтропии.

Термин нормировка будет дальше встречаться часто. Это про­цедура преобразования некоторой величины в необходимый для исследователя вид. Она нужна для того, чтобы какие-то показате­ли/коэффициенты/ индексы изменялись либо от 0 до 1, либо от -1 до +1. Тогда делается возможным сравнение их значений, получен­ных при разных условиях, например, для различных совокупностей объектов.

На практике пользуются в сравнительном контексте только од­ной мерой качественной вариации, ибо каждая мера отражает свое собственное понимание вариации. Потому значения, полученные по разным мерам, не имеет смысла сравнивать.

Date: 2015-09-24; view: 598; Нарушение авторских прав