
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Коэффициент корреляции
|
|
Теснота связи в корреляционной зависимости (5.11) характеризуется параметром  . Однако его величина зависит от единиц измерения переменных, что очень неудобно. Разделим обе части равенства (5.11) на
. Однако его величина зависит от единиц измерения переменных, что очень неудобно. Разделим обе части равенства (5.11) на  и представим уравнение в эквивалентном виде:
и представим уравнение в эквивалентном виде:
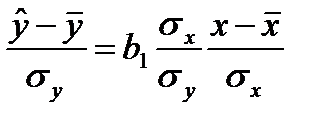 . (5.16)
. (5.16)
Величина

 (5.17)
(5.17)
называется коэффициентом корреляции Пирсона и показывает на сколько величин  изменится в среднем
изменится в среднем 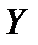 , когда
, когда  увеличится на одно
увеличится на одно 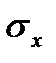 .
.
Коэффициент корреляции характеризует близость к линейной зависимости между двумя переменными.
Учитывая (5.12), формулу (5.17) для  представим в виде, удобном для практических расчетов:
представим в виде, удобном для практических расчетов:
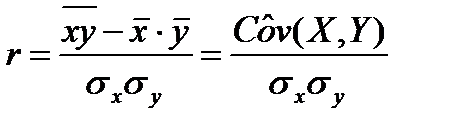 , (5.18)
, (5.18)
где  выборочные стандартные отклонения.
выборочные стандартные отклонения.
 находим по формуле (5.13), а
находим по формуле (5.13), а 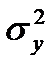 по формуле:
по формуле:
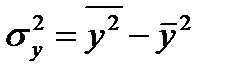 . (5.19)
. (5.19)
Коэффициент корреляции принимает значения 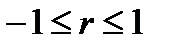 (Рис. 5.2.). Чем ближе
(Рис. 5.2.). Чем ближе 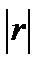 к единице, тем теснее связь. Если
к единице, тем теснее связь. Если  связь называется прямой (положительная корреляция), если
связь называется прямой (положительная корреляция), если 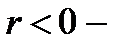 обратной (отрицательная корреляция). При
обратной (отрицательная корреляция). При 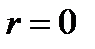 линейная корреляционная связь отсутствует.
линейная корреляционная связь отсутствует.
 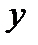 
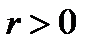 • • • • 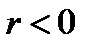 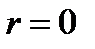 • • • • • • •
• • • • •
• •
• • • • • • •
• • • • •
• •
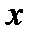  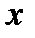 Рис. 5.2.
Рис. 5.2.
|
Иногда требуется оценить значимость коэффициента корреляции  (5.18). При этом исходят из того, что при отсутствии корреляционной связи статистика
(5.18). При этом исходят из того, что при отсутствии корреляционной связи статистика  имеет
имеет  распределение Стьюдента с
распределение Стьюдента с  степенями свободы.
степенями свободы.
Коэффициент корреляции 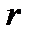 значим на уровне
значим на уровне 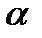 (т.е. гипотеза о равенстве генерального коэффициента корреляции нулю отвергается), если
(т.е. гипотеза о равенстве генерального коэффициента корреляции нулю отвергается), если
 , (5.20)
, (5.20)
где 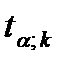 – квантиль распределения Стьюдента с
– квантиль распределения Стьюдента с  степенями свободы и уровнем значимости
степенями свободы и уровнем значимости 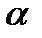 .
.
Коэффициент детерминации.
Наиболее эффективной оценкой адекватности регрессионной модели является коэффициент детерминации 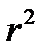 . Его величина показывает, какая доля вариации зависимой переменной обусловлена вариацией факторной переменной. Пределы изменения коэффициента детерминации
. Его величина показывает, какая доля вариации зависимой переменной обусловлена вариацией факторной переменной. Пределы изменения коэффициента детерминации  .
.
Критерий значимости уравнения парной регрессии или самого коэффициента детерминации может быть записан в виде
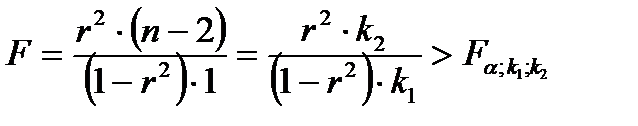 , (5.21)
, (5.21)
где  уровень значимости;
уровень значимости;
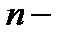 число наблюдений;
число наблюдений;
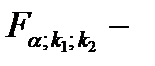 табличное значение
табличное значение 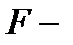 критерия Фишера-Снедекора, определенное на уровне значимости
критерия Фишера-Снедекора, определенное на уровне значимости 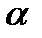 при
при 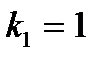 и
и  степенях свободы.
степенях свободы.
Пример 5.2.По данным табл. 5.1 вычислить коэффициенты корреляции и детерминации между переменными  и и  , оценить их значимость на уровне , оценить их значимость на уровне 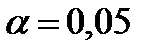 .
1) Ранее было вычислено .
1) Ранее было вычислено  ; следовательно ; следовательно  .
По формуле (5.19) находим .
По формуле (5.19) находим  .
Подставляем полученные значения в (5.18): .
Подставляем полученные значения в (5.18):  ,
то есть связь между переменными достаточно тесная.
Коэффициент детерминации ,
то есть связь между переменными достаточно тесная.
Коэффициент детерминации   .
Доля вариации 0,8 обусловлена вариацией фактора.
2) Статистика (5.20) равна .
Доля вариации 0,8 обусловлена вариацией фактора.
2) Статистика (5.20) равна 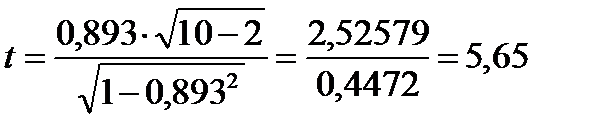 По таблицам
По таблицам 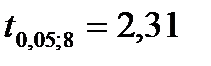 . Т.к. . Т.к. 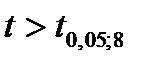 , то коэффициент корреляции значим.
Статистика (5.21) , то коэффициент корреляции значим.
Статистика (5.21)  .
Табличное значение .
Табличное значение 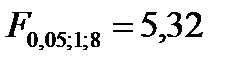 . Т.к. . Т.к. 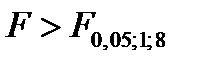 , то коэффициент детерминации и уравнение регрессии значимы. , то коэффициент детерминации и уравнение регрессии значимы.
|
Date: 2015-09-24; view: 457; Нарушение авторских прав