
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Оценка вероятности или доли элементов генеральной совокупности, обладающих определенным признаком
|
|
Выборочная доля (или оценка вероятности) определяется как отношение числа 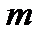 элементов выборки с изучаемым признаком к её общему объёму
элементов выборки с изучаемым признаком к её общему объёму 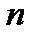 :
:
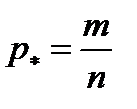 . (4.12)
. (4.12)
Выборочная дисперсия доли определяется величиной
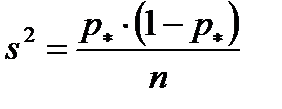 . (4.13)
. (4.13)
Величина предельной ошибки для доли равна:
· повторная выборка
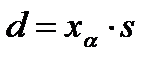 , (4.14)
, (4.14)
· бесповторная выборка
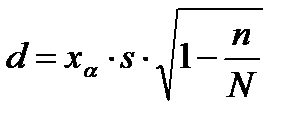
 . (4.15)
. (4.15)
Минимальный объём выборки, который обеспечивает требуемую точность, находят по формуле
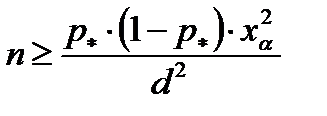 . (4.16)
. (4.16)
Пример 4.4. Имеется совокупность 10 000 деталей, произведенных на двух предприятиях. Для определения доли деталей, произведенных на первом предприятии, осуществили случайный бесповторный отбор 100 деталей. В выборке оказалось 20 деталей, произведенных на первом предприятии. Определить:
1) двусторонний доверительный интервал для доли, если уровень значимости 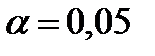 ;
2) требуемый объем выборки, если предельная ошибка ;
2) требуемый объем выборки, если предельная ошибка 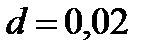 .
Решение.
1) Выборочную долю и дисперсию определяем по (4.12) и (4.13): .
Решение.
1) Выборочную долю и дисперсию определяем по (4.12) и (4.13):
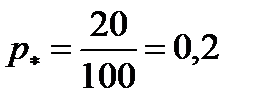 ; ; 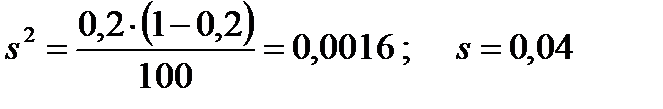 .
Предельную ошибку находим по (4.15) для .
Предельную ошибку находим по (4.15) для 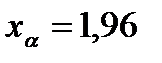
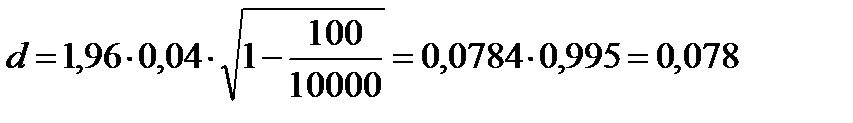 .
Как видно для условий примера практически нет разницы между повторным и бесповторным отбором.
Левая и правая границы равны: .
Как видно для условий примера практически нет разницы между повторным и бесповторным отбором.
Левая и правая границы равны:
 .
Можно утверждать, что с вероятностью 0,95 выполняется .
Можно утверждать, что с вероятностью 0,95 выполняется 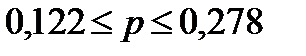 .
2) Если .
2) Если 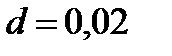 и и 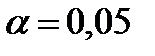 , то получим (9.16): , то получим (9.16):
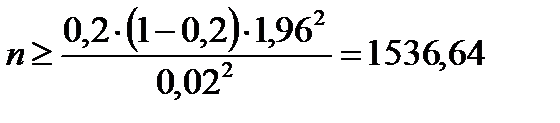 ; то есть ; то есть 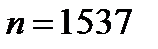 . .
|
Контрольные вопросы
1. Что такое точечная оценка?
2. Какие выборки считаются малыми?
3. Что такое интервальная оценка?
4. Как определяется необходимое количество измерений?
5. Способы формирования выборки.
6. Что такое повторная выборка?
7. Что такое правосторонний интервал?
8. Что такое двусторонний интервал?
Date: 2015-09-24; view: 483; Нарушение авторских прав