Показатели конкуренции

Для оценки интенсивности конкуренции используется показатель – индекс Герфиндаля, вычисляемый на основе данных о доле производства (или доходов) отдельных групп в совокупном объёме производства (или доходов):

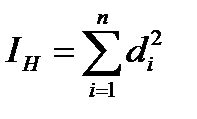(3.14)

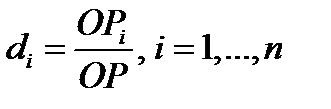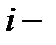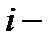где − доля й организации в общем объеме реализации (производства) продукции заданного ассортимента; − объем реализации го предприятия отрасли; общий объем реализации предприятий отрасли.

Индекс Герфиндаля увеличивается по мере роста концентрации в отрасли и достигает при чистой монополии 1. В отрасли (на рынке), где действуют 100 равномощных предприятий с равными долями, .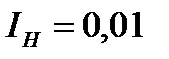

Индекс Герфиндаля не учитывает ранги предприятий. Этого недостатка лишен индекс Розенблюта, который рассчитывается с учетом порядкового номера предприятия, полученного на основе ранжирования долей от максимума к минимуму:

. (3.15)

Индекс Розенблюта изменяется от 0 до 1, причем равен 1 при чистой монополии.

3.4. Показатели концентрации.

Для оценки неравномерности распределения объёма изучаемого признака между группами абсолютные показатели числа элементов в группе (например, число банков и городов) и размера изучаемого признака (например, прибыль банка или численность населения) выражают в относительных показателях – в долях или процентах к итогу. Затем рассчитывают два ряда накопленных относительных частот. Кривая кумулятивных итогов для двух отдельных групп признака (например, число городов и численность населения, число банков и их прибыль) называется кривойЛоренца.

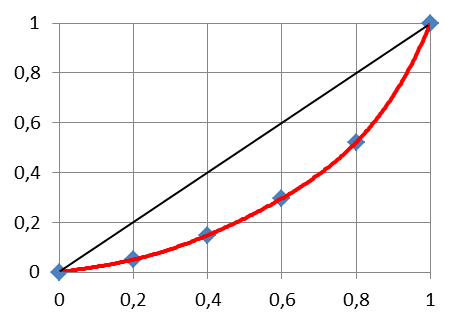
Рис. 3.1. Кривая Лоренца.

Для построения графика концентрации, т.е. кривой Лоренца, по оси абсцисс откладывают накопленные доли общего числа элементов совокупности (например, накопленные доли городов), а по оси ординат - накопленные доли по объёму изучаемого показателя (доли численности населения).

Чем дальше линия фактической концентрации (кривая Лоренца), построенная по указанным координатам, отклоняется от диагонали квадрата – линии равномерного распределения, тем выше уровень концентрации, т.е. тем более неравномерно распределен объём изучаемого показателя между единицами (группами) статистической совокупности. Чем ближе кривая Лоренца к прямой (диагонали квадрата), тем распределение признака более равномерное, т.е. концентрация меньше (Рис. 3.1).

Сопоставления кривых Лоренца за разные периоды позволяет выявить тенденции в неравномерности распределения объёма признака между группами. Такие сопоставления широко распространены в статистике, например, изучение распределения объёма денежных доходов между различными группами населения, анализ степени концентрации банковского капитала, сравнение концентрации объёма производства в различных отраслях промышленности и т.д.

Для количественного измерения концентрации используется показатель, называемый коэффициентом (индексом) Джини 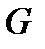, т.е. отношение площади , ограниченной линией равномерного распределения (диагональ квадрата) и кривой Лоренца, к половине площади квадрата:

.

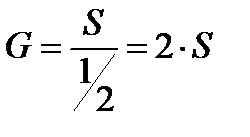Для равномерного распределения коэффициент Джини равен нулю, в условиях же полной концентрации он равен 1. Коэффициент Джинирассчитывается по формуле:

, (3.16)

где и 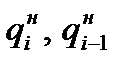- накопленные суммы удельных весов единиц распределения и кумулятивные итоги объёмного показателя, представленные по осям абсцисс и ординат, соответственно, в форме обычных относительных величин – не процентов.

Если 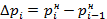одинаковы для всех и равны 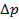, то формула (3.16) примет вид:

,

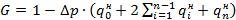а учитывая, что и , окончательно:

(3.17)

Пример 3.4.Определить коэффициент Джини для распределения общего объема денежных доходов населения, используя данные по 20-процентным группам населения за 2009 г.: 20-процентные группы населения: Удельный вес населения, Накопленная сумма удельных весов, Доля доходов Накопленная сумма доли доходов, 1 (с наименьшими доходами) 0,2 0,2 0,051 0,051   0,2 0,4 0,098 0,149   0,2 0,6 0,148 0,297   0,2 0,8 0,225 0,522 5 (с наибольшими доходами) 0,2 1,0 0,478 1,0 По формуле (3.17) получаем: . Для сравнения, по данным Росстата коэффициент Джини за 2010 год равен 0,42.

Контрольные вопросы

1. Что показывает коэффициент вариации?

2. Какие выборки считаются малыми?

3. Что такое дисперсия?

4. Сформулируйте нуль-гипотезу в дисперсионном анализе.

5. В какой шкале измеряется фактор в дисперсионном анализе?

6. Сформулируйте альтернативную гипотезу в дисперсионном анализе.

7. Что такое коэффициент детерминации?

8. Что измеряет индекс Герфиндаля?

9. Для чего применяется коэффициент Джини?

10. Что такое кривая Лоренца?

Date: 2015-09-24; view: 608; Нарушение авторских прав
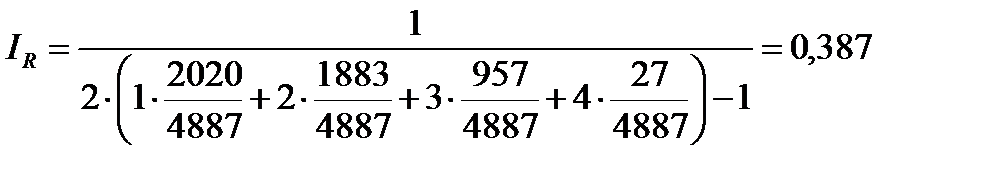
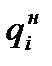
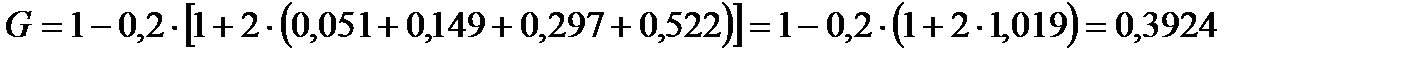