
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Анализ связи альтернативных признаков
|
|
Тесноту связи в случае анализа альтернативных признаков можно оценивать посредством коэффициента ассоциации Юла и коэффициента контингенции Пирсона.
Для расчета коэффициентов используется таблица взаимной сопряженности (таблица «четырех полей»):
| Признаки | А (да) |  (нет) (нет)
| Итого |
| В (да) | a | b | a + b |
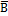 (нет) (нет)
| с | d | c + d |
| Итого | a + c | b + d | n |
Здесь а, b, c, d – частоты взаимного сочетания (комбинации) двух альтернативных признаков А и В; n - общая сумма частот.
Коэффициент ассоциации вычисляется по формуле:
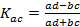 . (5.44)
. (5.44)
При  между изучаемыми качественными признаками существует корреляционная связь.
между изучаемыми качественными признаками существует корреляционная связь.
В случае, когда один из показателей таблицы отсутствует, величина коэффициента ассоциации будет равна единице, что дает завышенную оценку тесноты связи. В этом случае необходимо использовать коэффициент контингенции:
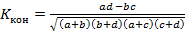 . (5.45)
. (5.45)
Нужно иметь в виду, что для одних и тех же данных коэффициент контингенции (изменяется от - 1 до +1) всегда меньше коэффициента ассоциации.
Пример 5.9.Оценить тесноту связи между атрибутивными признаками рабочих предприятия по данным таблицы:
Коэффициент ассоциации (5.44):
Величина Коэффициент контингенции (5.45):
|
Контрольные вопросы
1. Что такое коэффициент корреляции?
2. Как проверяется значимость коэффициента корреляции?
3. Что такое уравнение регрессии?
4. Какая связь называется корреляционной?
5. Какие показатели используются для оценки связи ранговых переменных?
6. Какие показатели используются для оценки связи атрибутивных переменных?
7. Для чего используется коэффициент ассоциации Юла?
8. Что такое коэффициент контингенции?
9. Для каких переменных можно построить уравнение регрессии?
10. Что такое и когда применяется коэффициент Кендэлла?
11. Когда применяются коэффициенты Чупрова и Крамера?
Date: 2015-09-24; view: 555; Нарушение авторских прав
 .
.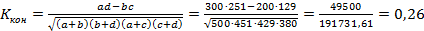 .
.