
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Оценка математического ожидания (средней величины)
|
|
Пусть распределение значений количественного признака в большой выборке (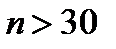 ) известно и записано в табличной форме:
) известно и записано в табличной форме:
Значение, 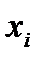
| Частота, 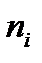
|
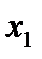
 …
…

| 
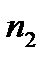 …
…
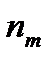
|
| Итого | 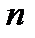
|
Выборочные среднее и дисперсия рассчитываются по формулам:
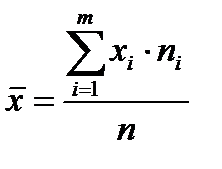 (4.1)
(4.1)
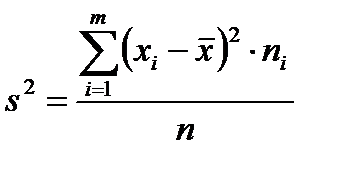 (4.2)
(4.2)
Величины  и
и 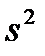 являются оценками параметров генеральной совокупности: математического ожидания
являются оценками параметров генеральной совокупности: математического ожидания  и дисперсии
и дисперсии  . Оценка
. Оценка  является случайной величиной, распределенной по нормальному закону. Величина
является случайной величиной, распределенной по нормальному закону. Величина 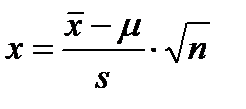 является центрированной (математическое ожидание равно нулю) и нормированной (дисперсия равна 1), поэтому для нахождения квантилей распределения
является центрированной (математическое ожидание равно нулю) и нормированной (дисперсия равна 1), поэтому для нахождения квантилей распределения 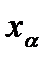 можно использовать таблицы функции распределения стандартного нормального распределения.
можно использовать таблицы функции распределения стандартного нормального распределения.
Истинное значение параметра  можно оценить при помощи доверительного интервала, который его включает
можно оценить при помощи доверительного интервала, который его включает
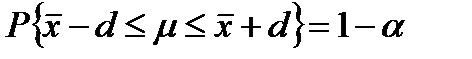 , (4.3)
, (4.3)
где  доверительная вероятность (надежность оценки), а
доверительная вероятность (надежность оценки), а
 уровень значимости, то есть вероятность ошибки.
уровень значимости, то есть вероятность ошибки.
Величина предельной ошибки равна:
· повторная выборка
 (4.4)
(4.4)
· бесповторная выборка

 . (4.5)
. (4.5)
Если объем генеральной совокупности существенно больше объема выборки, либо неизвестен, то пользуются формулой (4.4).
Средние ошибки выборки находят по формулам
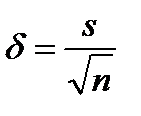 и
и 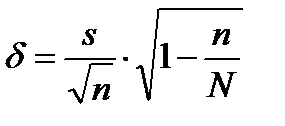 . (4.6)
. (4.6)
Интервал может быть двусторонним, либо односторонним.
Пример 4.1.Произведены измерения признака, распределенного на элементах генеральной совокупности неизвестного объема. Результаты измерений и вычислений приведены в таблице.
Точечные оценки находим по формулам (4.1) и (4.2).
· правосторонний интервал, По таблице нормального распределения находим По формуле (4.4) найдем Следовательно, · левосторонний интервал, Проводим те же вычисления и находим: · двусторонний интервал, Так как интервал двусторонний, квантиль распределения находим для По формуле (4.4) найдем Вычисляем левую и правую границы интервала: Получили: |
Если объем выборки небольшой 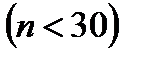 , то методика расчета доверительных интервалов немного изменяется. Для сгруппированных данных выборочное среднее определяем, как и ранее (4.1), а дисперсию по формуле:
, то методика расчета доверительных интервалов немного изменяется. Для сгруппированных данных выборочное среднее определяем, как и ранее (4.1), а дисперсию по формуле:
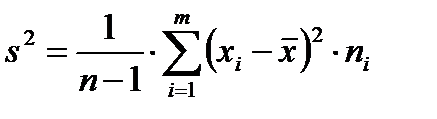 . (4.7)
. (4.7)
Для не сгруппированных данных используем формулы:
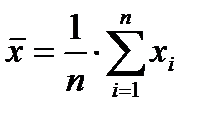 (4.8)
(4.8)
 (4.9)
(4.9)
Величина 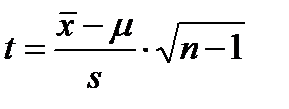 описывается стандартным
описывается стандартным 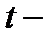 распределением Стьюдента с
распределением Стьюдента с 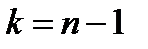 степенями свободы, поэтому для нахождения квантилей распределения
степенями свободы, поэтому для нахождения квантилей распределения  используют таблицы
используют таблицы  распределения (Приложение 2).
распределения (Приложение 2).
Предельная ошибка для повторной выборки будет равна

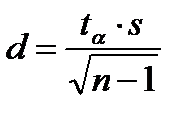 . (4.10)
. (4.10)
Пример 4.2.Произведены измерения признака, распределенного на элементах генеральной совокупности неизвестного объема. Результаты измерений и вычислений приведены в таблице.
По формулам (4.1) и (4.7) получаем точечные оценки.
· правосторонний интервал, По таблице степеней свободы По формуле (4.10) найдем Следовательно, · левосторонний интервал, Находим: · двусторонний интервал, Для двусторонней критической области, квантиль распределения По формуле (4.10) найдем Вычисляем левую и правую границы интервала: Получили: |
Если задана предельная ошибка и доверительная вероятность, из формул (4.4) и (4.10) можно найти необходимое количество измерений (объем выборки). Например, из (4.4) при заданных  находим:
находим:
 (4.11)
(4.11)
Пример 4.3.В условиях Примера 4.1 определить необходимое число измерений, если 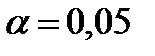 и и 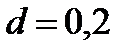 . Из таблиц для двустороннего интервала находим . Из таблиц для двустороннего интервала находим 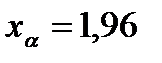 . По формуле (4.11) получаем . По формуле (4.11) получаем 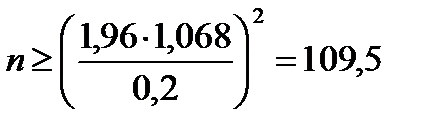 ; то есть ; то есть  . .
|
Date: 2015-09-24; view: 483; Нарушение авторских прав
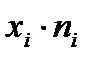
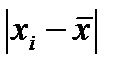
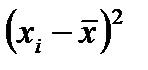

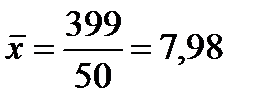 ;
; 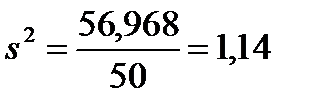 ;
; 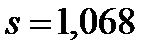 .
.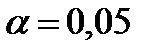 .
.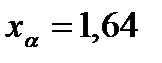 .
. .
. с вероятностью 0,95.
с вероятностью 0,95. с вероятностью 0,95.
с вероятностью 0,95. :
: 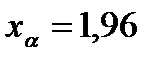 .
. .
. ;
;  .
.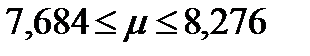 с вероятностью 0,95.
с вероятностью 0,95.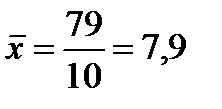 ;
; 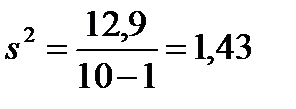 ;
;  .
.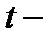 распределения для односторонней критической области и числа
распределения для односторонней критической области и числа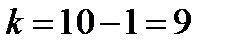 находим
находим  .
. .
.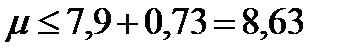 с вероятностью 0,95.
с вероятностью 0,95.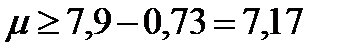 с вероятностью 0,95.
с вероятностью 0,95.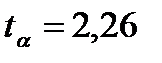 .
. .
.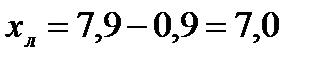 ;
; 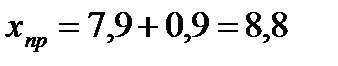 .
. с вероятностью 0,95.
с вероятностью 0,95.