
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Коэффициенты ранговой корреляции
|
|
В практике встречаются случаи, когда необходимо установить тесноту связи между порядковыми (ранговыми) переменными (например, качество жилищных условий, тестовые баллы и т.п.). В этом случае объекты анализа упорядочивают или ранжируют по степени выраженности измеряемых переменных. Если объекты ранжированы по двум признакам, то имеется возможность оценить тесноту связи между переменными, т.е. тесноту ранговой корреляции. Коэффициенты корреляции для этого случая были предложены К. Спирмэном и М. Кендэлом.
Коэффициент ранговой корреляции Спирмена находят по формуле
 , (5.33)
, (5.33)
где 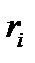 и
и  ранги
ранги  го объекта по переменным
го объекта по переменным 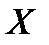 и
и  ;
; 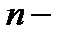 число пар наблюдений.
число пар наблюдений.
Если ранги всех объектов равны, т.е. при полной прямой связи, 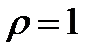 . При полной обратной связи, когда ранги объектов по двум переменным расположены в обратном порядке,
. При полной обратной связи, когда ранги объектов по двум переменным расположены в обратном порядке, 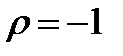 .
.
Иногда сталкиваются со случаями, когда несколько объектов имеют одинаковое значение признака. Тогда всем этим объектам присваивают средний ранг. Например, два объекта 3 и 4 оказались равными, тогда каждому приписывается ранг 3,5.
При проверке значимости 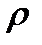 исходят из того, что при
исходят из того, что при  статистика
статистика
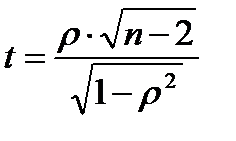 (5.34)
(5.34)
имеет 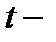 распределение Стьюдента с
распределение Стьюдента с 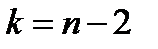 степенями свободы. Поэтому
степенями свободы. Поэтому 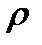 значим на уровне значимости
значим на уровне значимости  , если
, если 
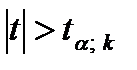 , где
, где 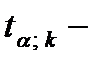 табличное значение
табличное значение  критерия Стьюдента.
критерия Стьюдента.
Пример 5.4.По результатам тестирования 10 студентов по двум дисциплинам А и В на основе набранных баллов получены следующие ранги (Табл. 5.3). Вычислить коэффициент ранговой корреляции Спирмена и проверить его значимость на уровне  .
Таблица 5.3. .
Таблица 5.3.
По формуле (5.33) Проверим значимость По таблицам найдем Т.к. |
Коэффициент Спирмена может быть использован и для оценки тесноты связи между обычными количественными переменными. Достоинство  заключается в том, что не требуется нормального распределения переменных, линейной связи между ними. Однако, при переходе от первоначальных значений переменных к их рангам теряется часть информации.
заключается в том, что не требуется нормального распределения переменных, линейной связи между ними. Однако, при переходе от первоначальных значений переменных к их рангам теряется часть информации.
Чем теснее связь, тем ближе коэффициент корреляции Спирмена  к коэффициенту парной корреляции
к коэффициенту парной корреляции 
Пример 5.5.По данным примера 5.1 вычислить коэффициент ранговой корреляции Спирмена и проверить его значимость на уровне  . .
По формуле (5.33) Проверим значимость По таблицам найдем Т.к. |
Коэффициент ранговой корреляции Кендэлла находят по формуле
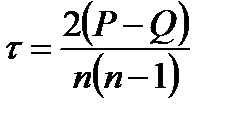 , (5.35)
, (5.35)
где 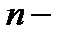 число пар наблюдений;
число пар наблюдений; 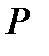 и
и 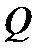 , соответственно, число согласованных и несогласованных пар рангов
, соответственно, число согласованных и несогласованных пар рангов 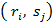 для всех
для всех 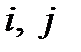 , таких, что
, таких, что 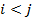 . Здесь пары называются согласованными, если оба значения одной пары одновременно больше или меньше обоих значений другой. В противном случае пары называются несогласованными.
. Здесь пары называются согласованными, если оба значения одной пары одновременно больше или меньше обоих значений другой. В противном случае пары называются несогласованными.
Коэффициент Кендэлла изменяется в пределах:  .
.
Для проверки значимости сначала вычисляют величину
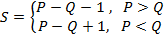 , (5.36)
, (5.36)
а затем статистику
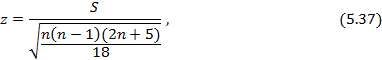
которая имеет нормальное распределение. Критическое значение  берем из таблицы стандартного нормального распределения для двусторонней критической области при уровне значимости α. Если
берем из таблицы стандартного нормального распределения для двусторонней критической области при уровне значимости α. Если 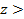
 , то коэффициент корреляции значим.
, то коэффициент корреляции значим.
Использование коэффициента ранговой корреляции Кендэлла продемонстрируем на данных Примера 5.4.
Пример 5.6.По результатам тестирования 10 студентов по двум дисциплинам А и В на основе набранных баллов получены следующие ранги.
Вычислить коэффициент ранговой корреляции Кендэлла и проверить его значимость на уровне Число согласованных пар рангов По формуле (5.35) Проверим значимость По (5.37) вычислим
По таблицам найдем |
Для оценки тесноты множественной связи ранговых переменных также применяют коэффициент конкордации, который будет подробно рассмотрен в Главе 8 (раздел 8.2.1).
Date: 2015-09-24; view: 566; Нарушение авторских прав

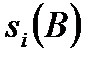
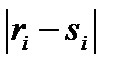
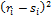
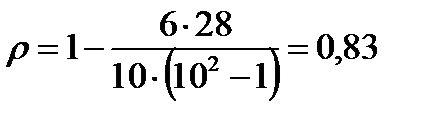 .
.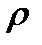 . По (5.34) вычислим
. По (5.34) вычислим  .
.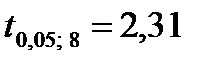 .
. , то коэффициент ранговой корреляции значим на уровне
, то коэффициент ранговой корреляции значим на уровне 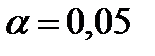 . Связь между оценками дисциплин довольно тесная.
. Связь между оценками дисциплин довольно тесная.
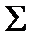
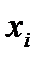



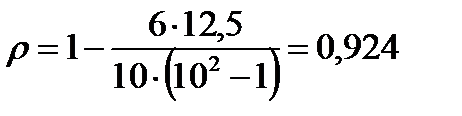 .
. .
. .
.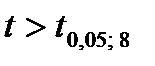 , то коэффициент ранговой корреляции значим на уровне
, то коэффициент ранговой корреляции значим на уровне 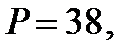 а число несогласованных пар –
а число несогласованных пар – 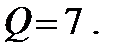
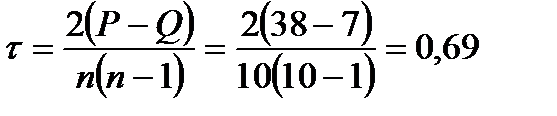 .
.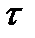 . По (5.36) вычислим
. По (5.36) вычислим 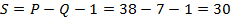 .
.
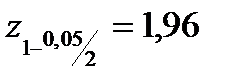 . Т.к.
. Т.к.