Теорема существования и единственности решения дифференциального уравнения

Если функция 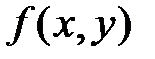и частная производная 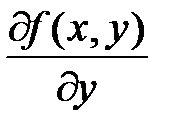непрерывны в некоторой области плоскости 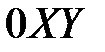, то для любой точки области существует единственное решение дифференциального уравнения, удовлетворяющее заданному начальному условию. Геометрически это означает, что через каждую точку области проходит одна единственная интегральная кривая.

Точки, в которых нарушается единственность решения, называются особыми точками дифференциального уравнения. Интегральная кривая, в каждой точке которой нарушается единственность решения задачи Коши, называется особым решением этого уравнения. Особое решение не может быть получено из общего решения ни при каких значениях произвольной постоянной.

Задача нахождения частного решения уравнения при условии может быть приближенно решена численными методами, например:

· Метод Эйлера. Значения искомой функции находят по формуле

;

Метод разложения в ряд Тейлора. Решение представляют в виде нескольких первых членов ряда:

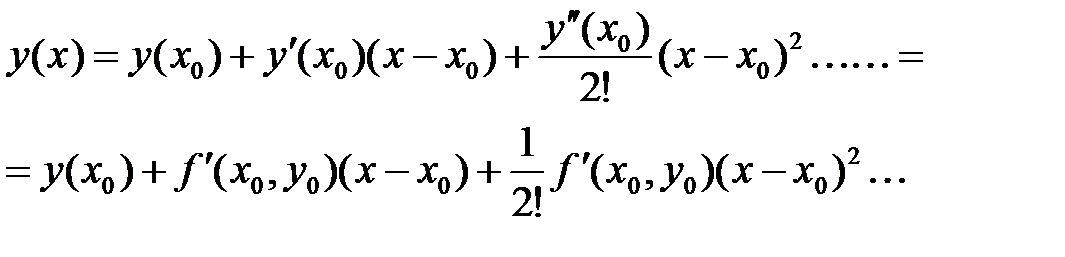
Date: 2015-09-24; view: 462; Нарушение авторских прав