
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Для векторного поля
|
|

Определены следующие дифференциальные операции первого порядка:
· Дивергенция векторного поля
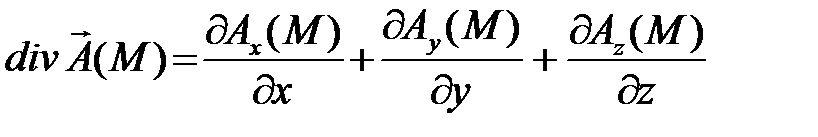 ;
;
· Ротор векторного поля  .
.
Интеграл от векторной функции вдоль кривой вводится согласно соотношению:
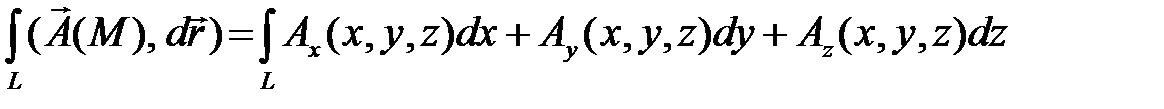 ,
,
а способ вычисления зависит от способа задания кривой, по которой ведется интегрирование:
· Кривая задана уравнением 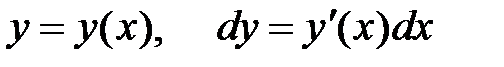 , а интеграл
, а интеграл



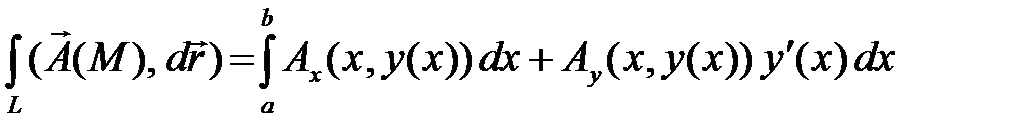 ;
;
· Кривая задана параметрически как векторная функция
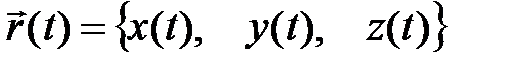 . Тогда интеграл находят по формуле
. Тогда интеграл находят по формуле

Условием потенциальности векторного поля дважды непрерывно дифференцируемого в односвязной области является условие: 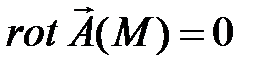 . Для такого поля определен потенциал
. Для такого поля определен потенциал  - скалярная функция такая, что
- скалярная функция такая, что  . В силу того, что интеграл от потенциального векторного поля вдоль кривой не зависит от контура интегрирования, одним из способов нахождения потенциала является интегрирование векторного поля по простейшему контуру, соединяющему две точки непрерывности поля линией, звенья которой параллельны координатным осям:
. В силу того, что интеграл от потенциального векторного поля вдоль кривой не зависит от контура интегрирования, одним из способов нахождения потенциала является интегрирование векторного поля по простейшему контуру, соединяющему две точки непрерывности поля линией, звенья которой параллельны координатным осям:
 .
.
Потоком векторного поля называют интеграл от векторной функции по поверхности  , ориентация которой определяется выбором направления нормали
, ориентация которой определяется выбором направления нормали  :
:
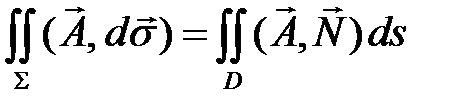 .
.
Поток векторного поля через замкнутую ориентированную поверхность находят с помощью теоремы Остроградского-Гаусса:
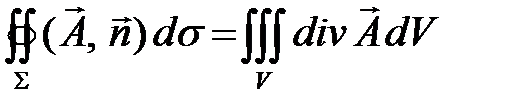 .
.
Циркуляцию дифференцируемого векторного поля (интеграл по замкнутому контуру) находим по теореме Стокса:
.
ЗАДАЧИ
1. Найти производные первого порядка векторных полей. Определить, какие из полей являются потенциальными. Для потенциальных полей найти потенциал.
а) 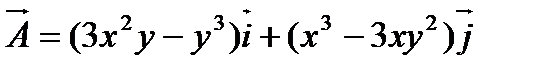 ;
;
б) 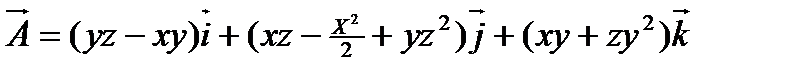 ;
;
е) 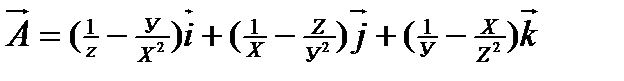
2. Найти работу векторных полей (из задачи 1 случаи а, б) при перемещении точки из М(1;0;0) в Р(0;2;0):
а) по прямолинейному отрезку МР;
б) по дуге эллипса 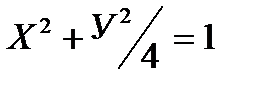 ;
;
Для потенциальных полей работу находить как разность потенциалов.
3. Для указанных векторных полей найти:
а) поток через поверхность s;
б) поток через замкнутую поверхность  (т. Остроградского–Гаусса);
(т. Остроградского–Гаусса);
в) циркуляцию по контуру L по теореме Стокса
1. 
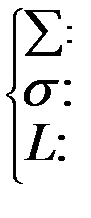
| Z = 4 – 2(x2+y2); z=2(x2+y2);
часть z=2, ограниченная линией пересечения параболоидов
линия пересечения  с z=2(y³0); y=0 (z³2); с z=2(y³0); y=0 (z³2);
|
2. 
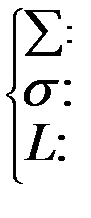
| у2+z2 = Rx; x=R; часть x=R, отсекаемая параболоидом линия пересечения параболоида с х = R; |
Контрольные вопросы
1.Дифференциальные операции первого порядка над векторными полями: дивергенция, ротор (вычисление в декартовой системе координат)
2. Оператор «набла» и выражение с помощью этого оператора градиента скалярного поля, дивергенции и ротора векторных полей
3. Дифференциальные операции второго порядка для векторных полей
4. Определения вихревого и потенциального векторных полей
5. Интеграл от векторной функции вдоль кривой. Свойства. Вычисление
6. Необходимое и достаточное условие потенциальности векторного поля
7. Свойства потенциального поля
8. Потенциал. Способ вычисления
9. Поток векторного поля через ориентированную поверхность. Свойства. Вычисление.
10. Теорема Остроградского-Гаусса. Определение дивергенции
11. Циркуляция векторного поля. Теорема Стокса
12. Найти работу векторного поля 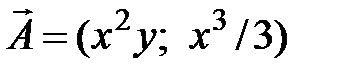 при перемещении материальной точки вдоль кривой при перемещении материальной точки вдоль кривой 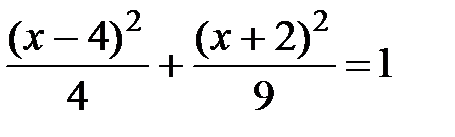 .
Ответы .
Ответы
а)
Самостоятельная работа РГР № 13 (0,456 ЗЕ) Дифференциальные уравнения
Срок выполнения 5- 8 недели
Содержание работы 1. Обыкновенные дифференциальные уравнения 1 порядка (с разделяющимися переменными, однородные, линейные, Бернулли);
2. Уравнения высших порядков, допускающие понижение порядка;
3. Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами
Литература [1, 2, 9, 16] Дифференциальные уравнения.
Функциональное уравнение
связывающие независимую переменную
Дифференциальные уравнения 1-го порядка разделяют на следующие типы: · Уравнения с разделяющимися переменными
· Однородные уравнения · Линейные уравнения
которые сводятся к разделению переменных подстановкой
· Уравнения Бернулли
Сводятся к линейным уравнениям подстановкой · Уравнения в полных дифференциалах
где точки
Порядок дифференциальных уравнений высших порядков можно понизить в следующих случаях: · · Уравнения вида · Уравнения вида · Уравнения, левая и правая части которых могут быть представлены как полные производные по переменной
Date: 2015-09-24; view: 880; Нарушение авторских прав |
 , б)
, б)  ; в)
; в)  ; ж)
; ж) 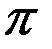 ;
;
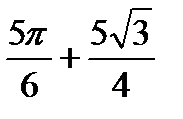 ;
Тройные интегралы:
;
Тройные интегралы:
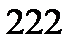 ;б)
;б) 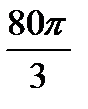 ;в)
;в) 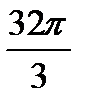 ;
ПрПрименение кратных интегралов
;
ПрПрименение кратных интегралов
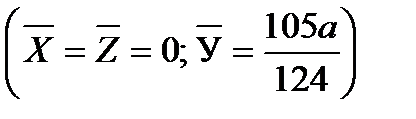 ;
;
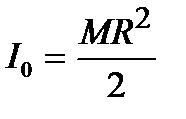 ; в)
; в) 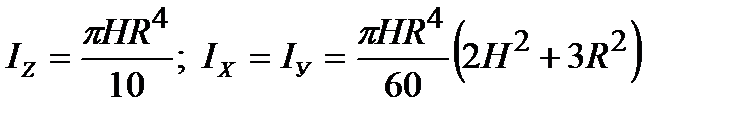 ;
Криволинейные и поверхностные интегралы 1 рода:
;
Криволинейные и поверхностные интегралы 1 рода:
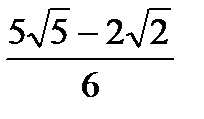 ;
;
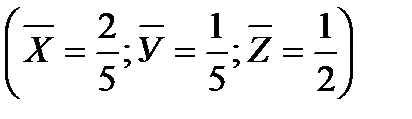 ;
;
 ;
;
 ;
;
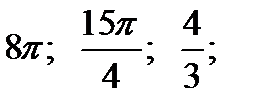 б)
б) 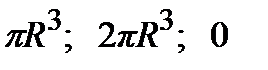

 , искомую функцию
, искомую функцию  и ее производные, называется дифференциальным уравнением порядка
и ее производные, называется дифференциальным уравнением порядка  (порядок уравнения - это порядок старшей производной, входящей в уравнение). Общим решением дифференциального уравнения называется функция
(порядок уравнения - это порядок старшей производной, входящей в уравнение). Общим решением дифференциального уравнения называется функция  , которая будучи подставлена в уравнение, обращает его в тождество. Здесь
, которая будучи подставлена в уравнение, обращает его в тождество. Здесь 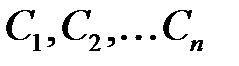 - произвольные постоянные, для определения которых задают начальные условия:
- произвольные постоянные, для определения которых задают начальные условия: 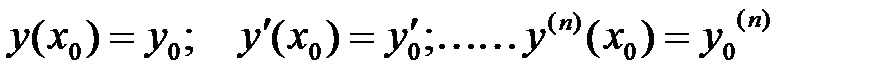 . Задачей Коши для дифференциального уравнения называют задачу нахождения частного решения по заданным начальным условиям. Частное решение определяет кривую на координатной плоскости, которую называют интегральной кривой. Уравнение
. Задачей Коши для дифференциального уравнения называют задачу нахождения частного решения по заданным начальным условиям. Частное решение определяет кривую на координатной плоскости, которую называют интегральной кривой. Уравнение  , которое определяет общее решение как неявную функцию, называют общим интегралом дифференциального уравнения.
, которое определяет общее решение как неявную функцию, называют общим интегралом дифференциального уравнения.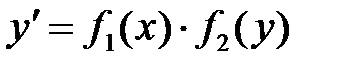 или
или 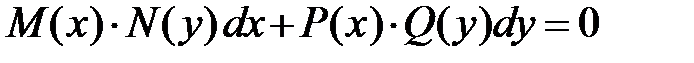 , которые можно непосредственно интегрировать, собрав с одной стороны от знака равенства выражения, зависящие только от одной переменной:
, которые можно непосредственно интегрировать, собрав с одной стороны от знака равенства выражения, зависящие только от одной переменной: или
или 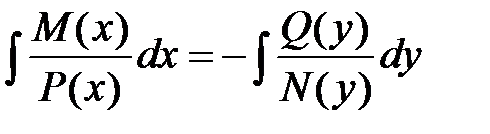 ;
;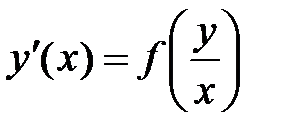 или
или  сводятся к уравнениям с разделяющимися переменными при помощи замены:
сводятся к уравнениям с разделяющимися переменными при помощи замены:  или
или 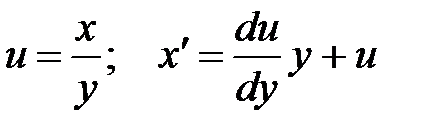 ;
;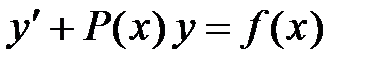 -по переменной
-по переменной 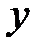 ,
,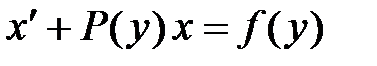 -по переменной
-по переменной  ,
, или
или 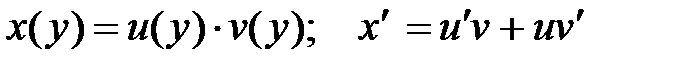 , а также методом вариации произвольной постоянной;
, а также методом вариации произвольной постоянной;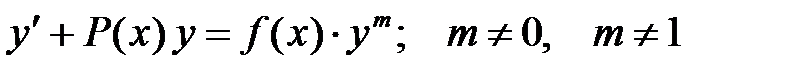

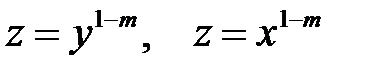 ;
;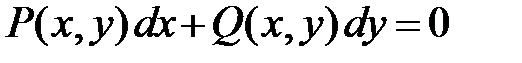 при условии
при условии 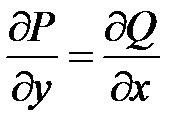 (условие существования полного дифференциала или условие потенциальности векторного поля
(условие существования полного дифференциала или условие потенциальности векторного поля 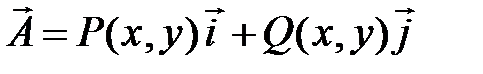 ) решаем путем восстановления функции – потенциала
) решаем путем восстановления функции – потенциала  такой, что
такой, что 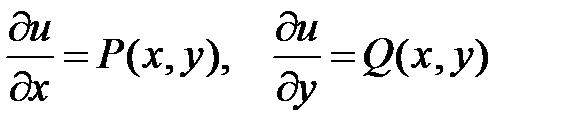 , каким-либо способом, например
, каким-либо способом, например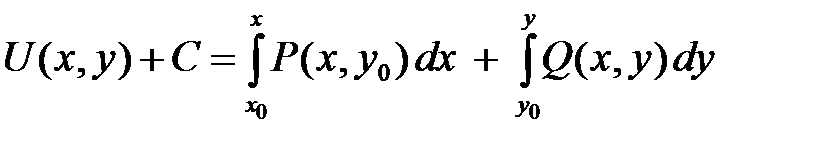 ,
,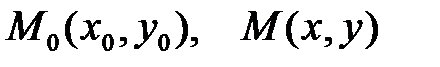 лежат в области непрерывности функций
лежат в области непрерывности функций 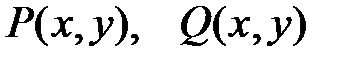 и их производных.
и их производных.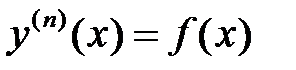 . Общее решение в этом случае находят путем
. Общее решение в этом случае находят путем  - кратного интегрирования;
- кратного интегрирования; :
:  ;
; :
: 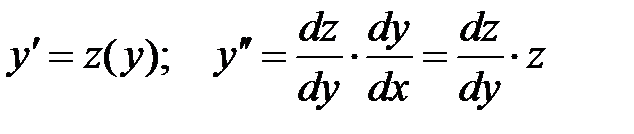 ;
;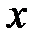 от некоторой функции. Интегрируя по переменной
от некоторой функции. Интегрируя по переменной 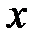 , получаем уравнение, порядок которого на единицу ниже порядка исходного уравнения.
, получаем уравнение, порядок которого на единицу ниже порядка исходного уравнения.