Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Тройные интегралы

⇐ ПредыдущаяСтр 2 из 26Следующая ⇒

 

Тройным интегралом от непрерывной функции 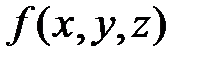по ограниченной замкнутой пространственной области 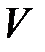называют предел последовательности интегральных сумм

 

.

 

Вычисление тройного интеграла в декартовой системе координат сводится к последовательному вычислению однократного интеграла по одной из координат и двойного интеграла по проекции объема 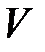на одну из координатных плоскостей. Если область интегрирования ограничена сверху и снизу гладкими поверхностями , и однозначно проектируется на плоскость в область 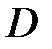, то интеграл вычисляют по формуле:

 

.

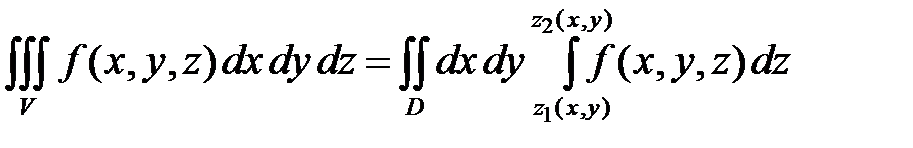В тех случаях, когда объем проектируется на координатную плоскость в круг или часть круга, используют криволинейные системы координат. Так в цилиндрической системе координат интеграл вычисляют согласно соотношению:

.

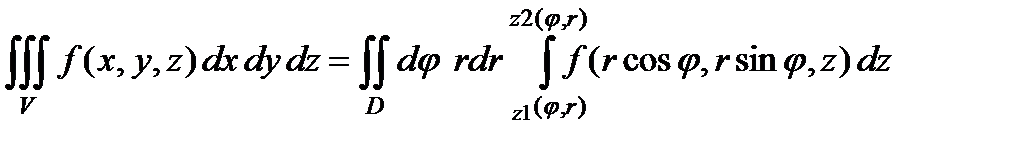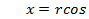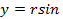φ φ
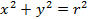
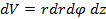
x
y

 

В тех случаях, когда пространственное тело ограничено сферическими поверхностями, удобно использовать сферическую систему координат, которая каждой точке пространства приписывает три координаты: полярный угол 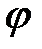, азимутальный угол и расстояние от начала координат до точки на сфере 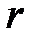. Тройной интеграл при этом представляется в виде:

 

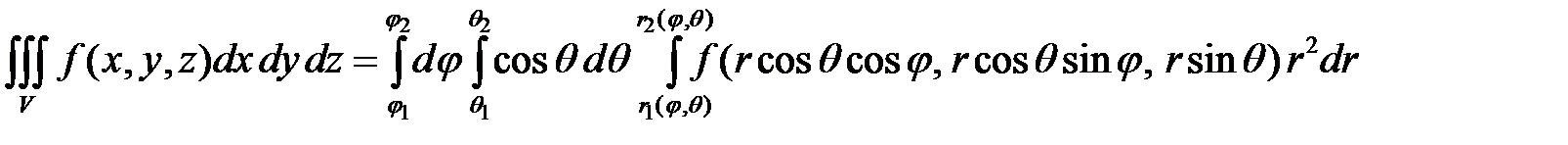
r
ϴ
φ
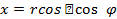
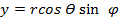
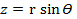
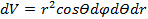
M (φ, ϴ, r)

 


⇐ Предыдущая12345678910Следующая ⇒





Date: 2015-09-24; view: 380; Нарушение авторских прав


mydocx.ru - 2015-2025 year. (0.008 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию