
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лекция 6
|
|
Тема. Структурная кристаллография (продолжение)
План
1. Кристаллографическая зона.
2. Межплоскостные расстояния.
3. Кристаллографические совокупности.
4. Расщепление совокупностей при понижении симметрии решетки.
5. Фактор повторяемости.
Серия семейств плоскостей параллельных одному направлению в решетке называется кристаллографической зоной, а само направление -осью зоны. Условие принадлежности плоскости (hkl) к кристаллографи-ческой зоне с осью [uvw] описывается условием зональности (4.5). Из ус-ловия зональности выводятся два следствия.
1. Если известны индексы двух пересекающихся плоскостей (h1k1l1j) и (h2k2l2), то легко найти символ [uvw] направления, совпадающего с ли-нией их пересечения.
Ясно, что [uvw] принадлежит (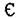 ) каждой из этих плоскостей, т.е.
) каждой из этих плоскостей, т.е.
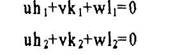
Это система 2-х уравнений с 3-мя неизвестными. Поскольку необходимо найти лишь соотношение u: v: w, то задача решается однозначно. Составляем матрицу коэффициентов
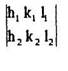
и находим
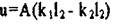 (вычерк.иваем 1-ый столбец),
(вычерк.иваем 1-ый столбец), 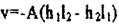 (вычеркиваем 2-ой столбец),
(вычеркиваем 2-ой столбец), 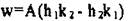 (вычеркиваем 3-ий столбец).
(вычеркиваем 3-ий столбец).
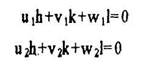 (4,6) (4,6)
|
А- неизвестный числовой множитель, который можно опустить. 2. Если известны индексы 2-х направлений 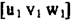 и
и 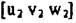 легко найти индексы плоскости (hkl), в которой они лежат. Очевидно
легко найти индексы плоскости (hkl), в которой они лежат. Очевидно
Из уравнений (4.6) определяем символ плоскости (hkl).
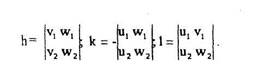
На рис.4.10 изображена кристаллографическая зона (hkl) и гномо-стереографические проекции плоскостей и стереографические проекции зоны (см.лаб.раб.№2).
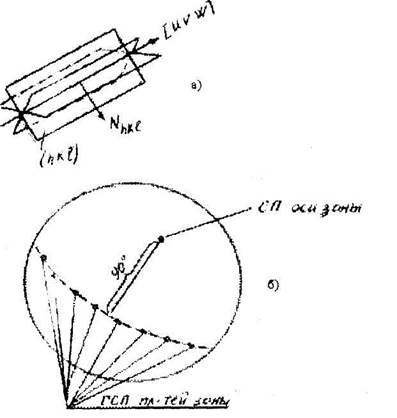
Ркс 4.10 Криспллографическая зонш (a) к ее ГСП (б)
Каждое семейство плоскостей характеризуется своим межплоскост-
ным расстоянием 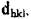 т.e. расстоянием между соседними параллельны-
т.e. расстоянием между соседними параллельны-
ми кристаллографически идентичными плоскостями семейства (hkl). В сложной решетке состоящей из разных атомов d - это расстояние между соседними плоскостями одной простой подрешетки, в узлах которой находятся идентичные атомы. Так, каждый атом базиса есть узел простой подрешетки. ГЦК решетка состоит из 4-х простых подрешеток.
Найдем математическую связь межплоскостного расстояния dhkl с индексами плоскости (рис.4.11).
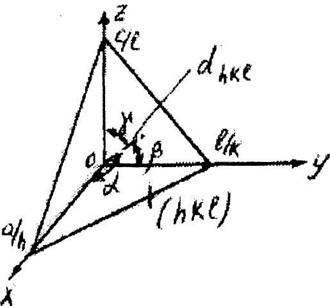
Рис. 4.11. К нахождению
| Для орторомбической сингонии |
Т.к. через начало координат "О" также проходит плоскость семейства, то перпендикуляр из начала координат на плоскость (hkl) и будет dhki-Заданная плоскость отсекает следующие координатные отрезки: a/h> b/k, с/1. Тогда направляющие косинусы нормали 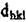 определятся как
определятся как
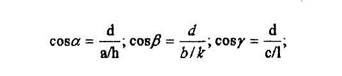
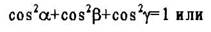
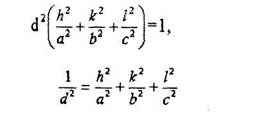
|
(4.7)
Из уравнения (4.7) видно, что чем больше индексы плоскости, тем меньше dhki- Чем больше индексы плоскости, тем ниже плотность их за-полнения атомами. Уравнение (4.7) для разных сингонии имеет следую-щий вид:
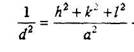
|
кубическая,
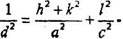
|
тетрагональная,
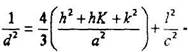
|
гексагональная.
Под совокупностью кристаллографических семейств плоскостей понимают группу семейств плоскостей, обладающих одинаковым, харак-терным расположением атомов, с одинаковыми физико-химическими свойствами, одинаковыми межплоскостными расстояниями и численно одинаковыми индексами в символе, отличающихся лишь порядком запи-си и знаком. Совокупность плоскостей обозначается фигурными скобками {hkl}.
Например, в кубической сингонии совокупность плоскостей куба {100} содержит 6 кристаллографически идентичных семейств плоскостей: (100), (100), (010), (010), (001) и (001). Если с помощью различных опера-ций симметрии повернуть 11.Р. так, что на месте плоскостей (100) встанут плоскости (001) или любые из других 4-х семейств, то новое положение решетки совпадет с исходным. В этом и состоит кристаллографическая
идентичность.
Основным признаком кристаллографически идентичных плоскостей является равенство межплоскостных расстояний. Отсюда количество кри-сталлографически идентичных плоскостей (семейств плоскостей) в дан-ной совокупности равно числу возможных перестановок местами и зна-ками индексов, не изменяющих величины 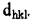
Рассмотрим те же 6 плоскостей. Для кубической сингонии для всех 6 семейств 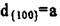 и они входят в одну совокупность.
и они входят в одну совокупность.
В случае тетрагональной сингонии
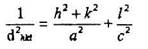
|
6 плоскостей распределяются по 2-ум совокупностям с разными межплоскостными расстояниями.
1. {100}: (100), (100), (010), (010); здесь 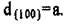
2. {001}: (001), и (001), здесь 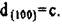
Таким образом, совокупность {100} в кубической сингонии расщеп-ляется на 2 совокупности {100} н {001} в тетрагональной сингонии, обладающей брлер низкой симметрией.
Дднако, следует заметить, что на расщепление влияет и характер индексов. Так, если рассмотреть совокупность {111}, то она не будет расщепляться в тетрагональной сингонии.
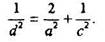
Количество семейств плоскостей в совокупности определяется фак-тором повторяемости - р. При расщеплении 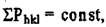 т.к. общее число плоскостей неизменно. Совокупность соответствующих плоскостей обра-зует простую форму. В табл.4.5 указан фактор повторяемости разных со-вокупностей в кристаллах кубической сннгонии.
т.к. общее число плоскостей неизменно. Совокупность соответствующих плоскостей обра-зует простую форму. В табл.4.5 указан фактор повторяемости разных со-вокупностей в кристаллах кубической сннгонии.
Факторповторяемости разных совокупностей в кристаллах ку-
бической сингонии
Табл.4.5.
| Индексы | hOO | hhO | hhh | hkO | hhk | hkl |
| Р |
Выводы
1. Условие зональности позволяет выяснить принадлежность систе-
мы плоскостей данной зоне.
2. С повышением индексов плоскости межплоскостное расстояние
уменьшается.
3. При понижении симметрии кристалла возможно расщепление од-
ной совокупности плоскостей на несколько.
ЛЕКЦИЯ 7
Тема Симметрия кристаллических решеток
План
1. Элементы симметрии открытых фигур (дисконтинуума).
2. Пространственные группы симметрии.
3. Главные направления и обозначение пространственных групп.
Ранее мы установили, что 32 точечных групп симметрии определяются набором поворотных и инверсионных осей, плоскостей симметрии и центра инверсии. Точечная группа определяет большинство физических свойств кристалла и его внешний облик. При переходе к рассмотрению симметрии пространственной решетки появляется новый
Э.С. трансляция. Трансляция в бесконечно протяженной решетке
(дальний порядок в расположении частиц) переводит систему точек в
идентичное положение. На рис.5.1 показано действие оси трансляции.

Рис, 5,1. Действие оси трансляции (АВ = ВС = СД=...)
При переносе на величину АВ вправо узел  ,
, 
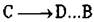 результате весь отрезок АВ сдвинется и бесконечный ряд узлов совместится сам с собой.
результате весь отрезок АВ сдвинется и бесконечный ряд узлов совместится сам с собой.
Такой параллельный перенос частицы на период идентичности вдоль данного направления называют, осью трансляции. Если осью трансляции подействовать на 32 класса симметрии, то набор независимых совокупностей Э.С. увеличится до 230 пространственных групп симметрии.
Э.С. + ось трансляции = новый Э.С.
Евграф Степанович Фёдоров (1896 г.) вывел 228 пространственных групп. 2 года спустя Шенфлис независимо от Федорова Е.С. получил 231
группу. Путем взаимной переписки они окончательно установили 230 пространственных групп симметрии или 230 различных систем расположения материальных частиц в пространстве. Все полученные сочетания Э.С. совместимы с условием существования П.Р.
Пространственной группой симметрии называют совокупность всех возможных элементов симметрии кристаллической структуры. Если точечная группа симметрии характеризует симметрию внешней формы кристалла, то пространственная группа определяет симметрию как внешней формы, так и внутренней структуры. Каждой точечной группе соответствует несколько пространственных групп. Это открытие по значимости является аналогом таблицы Менделеева.
Группы симметрии открытых фигур называют пространственными, поскольку данную комбинацию Э.С. можно встретить в бесконечном множестве точек П.Р. Пространственной группой называю совокупность Э.С. действующих на одну систему трансляции (ячейку Бравэ). По сингониям пространственные группы распределяются следующим образом:
-триклинная - 2,
- моноклинная -13,
- ромбическая - 59,
- тригональная - 25,
- тетрагональная - 68,
- гексагональная - 27,
-кубическая - 36..
Действие трансляции на Э.С. закрытых фигур дают новые Э.С. дисконтинуума: плоскости скользящего отражения и винтовые оси, На рис.5.2 показано действие плоскостей скользящего отражения разного типа. Плоскость скользящего отражения соответствует действию плоскости зеркального отражения и параллельного этой плоскости сдвига на долю трансляции (периода идентичности). На рис.5.2,а показано
действие плоскостей скользящего отражения типа "а" и "b", где трансляция - Т идет параллельно ребрам ячейки а и b на Т/2. Плоскость типа "с" дает трансляцию вдоль ребра [001].
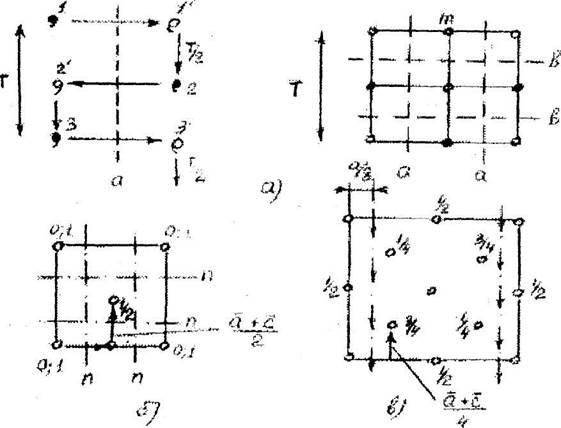
Рис. 5.2. Плоскость скользящего отражения
Величина сдвига в плоскости скользящего отражения соответствует половине осевой или диагональной трансляции. В табл.5.1 приведены величины трансляций для плоскостей скользящего отражения разного типа.
Date: 2015-09-24; view: 1673; Нарушение авторских прав