Fhc. 3.7. К выводу классов симметрии средней и высшей категории

Выводы

1. Тип кристаллической решетки и межатомной связи определяют
свойства кристаллов.

2. Характерной особенностью металлической связи является
электронный газ в котором "плавает" кристаллическая решетка.

3. Кристаллические структуры обладают анизотропией.

4. Свойства кристаллов могут быть векторными и скалярными.

ЛЕКЦИЯ 3

Тема. Симметрия кристаллов

План лекции

1. Понятие симметрии.

2. Элементы симметрии (э.с.) закрытых фигур (континуума).

3. Основные теорему о взаимодействии э.с.

4. Направления единичные и симметрично равные.

5. Виды симметрии.

6 Простые формы и комбинации.

Хотя понятием симметрии люди пользовались очень давно, математическая разработка учения о симметрии относится ко второй половине прошлого столетия и принадлежит двум выдающимся русским академикам Гадолину А.В. (1828 -1892 гг.) и Федорову КС.(1853-1919 г.г) Идеальные кристаллы имеют симметрию внешней формы.

Симметрия - это закономерное расположение равных фигур или частей фигур друг относительно друга в пространстве. Иначе - это свойство фигуры совмещаться с исходным положением в результате определенных пространственных перемещений. Для выяснения связи между структурой и анизотропией свойств необходимо уметь анализировать узоры (мотивы) повторения материальных частиц в пространстве, т е. определять степень симметрии кристалла и К.Р.

Для обнаружения симметрии используют элементы симметрии (э.с.) - вспомогательные геометрические образы (точки, прямые, плоскости). В закрытых фигурах - ограненных кристаллах могут присутствовать следующие э.с. (э.с. многогранников называют также э.с. континуума): центр инверсии - С, плоскость симметрии - Р, оси симметрии или поворотные оси - Ln, инверсионные оси Lin (см. лаб. раб.№1)

Э.с определяют большинство физических свойств кристалла и его форму В кристаллах возможны только оси симметрии 1,2,3,4,6 и

невозможны оси симметрии 5-го порядка и порядка больше, чем 6. Это обусловлено тем, что кристалл - это бесконечная система материальных частиц,симметрично повторяющихся в пространстве. Такие симметричные бесконечные ряды, сетки, решетки, непрерывно заполняющие пространство, несовместимы с осями 5,7 и других более высоких порядков.

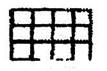
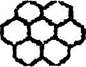
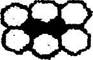
Действительно, плоские узловые сетки составленные из ромбов (2), квадратов (4), прямоугольников (2) и треугольников (3) покрывают всю плоскость без зазоров или пустот (рис 3.1.).

Рис. 3.1. Плоские сетки составленные из фигур с осями симметрии 2...8-го порядков

Но непрерывно заполнить плоскость 5-ти, 7-ми или 8-ми угольниками не удается - остаются зазоры. В системе материальных частиц наличие таких зазоров создавало бы возможность перемещения частиц, т.е. неустойчивость структуры. В случае заполнения плоскости 8-ми угольниками остаются зазоры в виде.квадратов. Но при этом изменяется симметрия атомной сетки. Здесь будет присутствовать только ось 4, т.к. восьмиугольник симметрично окружен лишь четырьмя квадратами.

Итак, внешняя форма кристаллов описывается следующими э.с: т, 1, 2, 3, 4, б, 3, 4, 6(так выглядит международная запись плоскости симметрии и поворотных осей симметрии).

В симметричных многогранниках операции симметрии сочетаются друг с другом и порождают новые э.с: 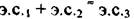(новый э.с). В

многогранниках э.с. всегда пересекаются в центре тяжести. Возможные сочетания э.с ограничены следующими теоремами. (Фактически существует только одна теорему Эйлера -теорема № 2, а все остальные являются следствиями). Теорема № 1.

Действие двух плоскостей симметрии, пересекающихся под углом («равносильно действию поворотной оси с элементарным углом поворота L2a Порядок оси равен 360/2а.

Pi+P₂=L_2a

Доказательство этой теоремы представлено на Рис.3,2. Как видно, последовательные отражения асимметричной фигурки (запятой) двумя плоскостями PiH Р₂, как в двух зеркалах эквивалентно повороту на угол 2а.

Рис. 3.2. К доказательству теоремы N 1

Теорема№2.

Равнодействующей двух пересекающихся поворотных осей является третья ось, проходящая через точку их пересечения (Рис.3. 3.).

1 2 3 L +L =L

Оси 2 лежат в плоскости чертежа и пересекаются под углом.
Поворот вокруг первой оси переводит фигуру А в положение Б, а поворот вокруг
второй оси - в положение В. Фигуру В можно получить поворотом

фигуры А в плоскости чертежа на угол 2а вокруг оси симметрии, проходящей через точку пересечения заданных осей.

Рис. 3.3. К доказательству теоремы N 2

Теорема 3.

Точка пересечения чётной оси симметрии с перпендикулярной ей плоскостью симметрии есть центр симметрии (Рис.3.4.)

Рис. 3.4. К доказательству теоремы N 3

Следствия: а)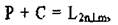

б)

в) , при наличии центра инверсии С.

На первой проекции показано действие оси 4, перпендикулярной плоскости чертежа, на второй - действие плоскости симметрии, совпадающей с плоскостью чертежа. Сочетание этих двух преобразований показано на третьей проекции. Как видно симметричные 8 точек обладают центром инверсии. В международных символах - 4/m указываются только порождающие (основные) э.с

Теорема 4.

Если есть ось L_n и вдоль неб проходит плоскость симметрии, то таких плоскостей будет п (рнс.3.5.).

Рис. 3.5. К доказательству теоремы N 4

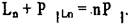
Плоскость 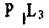переводит фигуру А в А¹. Поворот вокруг L₃

переводит фигурку А в Б и В, А¹ в Б¹ и В¹. Но каждая пара фигур Б и Б¹, В и В¹ связана между собой и отражением в плоскости симметрии, т.е. всего будет три плоскости Р.

Теорема 5.

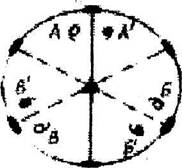
Если есть ось L_n и перпендикулярно этой оси проходит ось L₂, то всего таких осей будет 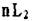, перпендикулярных 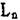(рис.3.6).

Рнс. 3.6. К доказательству теоремы N 5

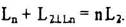
Пусть ось L₂, лежит в плоскости чертежа и перпендикулярна оси L₃, Тогда

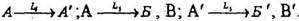
Видно, что каждая пара фигур Б и Б'

или В и В' связана между собой осью L₂, лежащей в плоскости чертежа.

Всего таких осей 3L₂. Эта теорема понятна и по самому определению оси симметрии: вокруг оси L_n любой объект симметрично повторяется п раз.

Взаимодействие Э.С. приводит к ограниченному числу сочетаний основных или порождающих Э.С, т.к. остальные будут просто повторяться. Вывод всех возможных сочетаний Э.С. для закрытых фигур был дан немецким ученым Гесселем ещё в 1830 г. Он доказал, что в кристаллах возможны лишь 32 вида (класса) симметрии. Однако его труды долгое время оставались незамеченными. В 1867 г. русский академик Гадолин А.З. независимо от Гесселя пришел к тем же результатам более простым математическим путем.

Видом симметрии кристалла называют полную совокупность набора его элементов симметрии. Познакомимся с общим принципом вывода гадолинских классов симметрии. Ось симметрии принимается за основной порождающий Э.С, к которому поочередно добавляются другие порождающие Э.С. Пусть ось L_n является единичным направлением, т.е. не повторяющимся в кристалле. Например, таким единичным направлением в гексагональной пирамиде является ось L₆. Каждая прямая, заданная косо к оси L₆ имеет, по крайней мере, 6 аналогичных симметрично расположенных прямых. Направления, повторяющиеся в кристалле и связанные Э.С. называются симметрично-равными. Так в кубе нет единичных направлений, а только симметрично-равные. Воздействуем на ось L_n такими Э.С, которые не переводили бы единичные направления в симметрично-равные (Рис.3.7.).Из рис.3.7,а выводим 5 возможных классов симметрии:

L₁, L₂, L₃, L₄, L₆. Полученные виды симметрии, состоящие только из одной оси симметрии называют примитивными.

Из рис.3.7, б имеем следующие классы: L₁C, L₂C, L₃С, L₄C, L₆C.

Учитывая теорему

получаем:

В результате получаем следующие классы симметрии, называемые центральными (действие центра инверсии С):

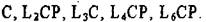
Fhc. 3.7. К выводу классов симметрии средней и высшей категории

Из рис.3.7,в для четных осей получаем тот же центральный вид. Для нечетных осей имеем инверсионно-примитивные классы Р>

В соответствии с теоремой анализ рис.3,7,г дает

планальные (или плоскостные) классы симметрии: Р, L₂2P, L₃3P, L₄4P, L₆6P.

На основании теоремы из Рис.3.7,д имеем новые пять

аксиальных, т.е. осевых классов симметрии:

Аналогичным образом, путем воздействия других дополнительных Э.С. на рассмотренные схемы получают все 32 класса симметрии. Например, если к схеме рис.3.7,6 добавить плоскость Р параллельную оси L_n, то будем иметь: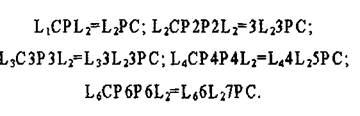

Или в международном обозначении:

Это планаксиальные классы симметрии. Все 32 класса сводятся в одну таблицу (см л.р.§ 1).Друппа классов симметрии обладающая одним или несколькими сходными Э.С. называется сингонией. Всего существует 7 сингоний: триклинная, моноклинная, ромбическая, тригональная, тетрагональная, гексагональная и кубическая. Т.к. все Э.С. закрытых фигур пересекаются в одно точке - центре тяжести фигуры классы симметрии часто называют точечными группами симметрии.

Пространственные решетки, относящиеся к кристаллам одной сингоний обладают элементарными ячейками с одинаковой симметрией.

Сингоний группируются в три категории: низшую, среднюю высшую. Низшая - нет осей порядка выше 2. Средняя характеризуется единственными осями Высшая - присутствует несколько осей

порядка выше 2, т.е. единичных направлений нет.

Некоторые примеры записи точечных групп:

622, 6mm, 6/m(mm) - гексагональная сингония, 23, 432, m3m - кубическая сингония,

4, 4,422,4mm - тетрагональная сингония. т

Выводы

Date: 2015-09-24; view: 703; Нарушение авторских прав