Лекция 5

Тема. Структурная кристаллография (продолжение)

План

1. Индексы плоскостей и направлений.

2. Основные кристаллографические соотношения.

3. Условие зональности.

Параллельные друг яругу плоскости и одинаково ориентированные в пространстве составляют семейство плоскостей, а параллельные направ-ления - семейство направлений. Такие плоскости или направления входя-щие в эти семейства кристаллографически идентичны и имеют одинаковые межплоскостные расстояния или периоды идентичности.

Индексы плоскостей (направлений) задают лишь ориентировку в пространстве данного семейства. Поскольку плоскости (направления) се-мейства кристаллографически равноценны их индексы должны быть оди-наковы. Использовать уравнения аналитической геометрии для записи бесконечного множества различно ориентированных в пространстве плос-костей и направлений невозможно.

Анализируя внешнюю форму кристаллов Рэне Гаюи (1820) показал, что отношения отрезков, отсекаемых двумя любыми гранями кристалла на трех пересекающихся его рёбрах, равны отношению целых и сравнительно малых чисел. Это так называемый закон целых чисел. Он бусловлен тем, что грани кристалла имеют наивысшую ретикулярную плоскость.

С учетом закона целых чисел Миллером был предложен удобный способ обозначения плоскостей, который нашел широкое распространение в кристаллографии. Под кристаллографическими индексами плоскости по-нимают три целых взаимно простых числа h, k, 1, обратно пропорциональ-ных отрезкам, отсекаемым на координатных осях. Отрезки измеряются в осевых единицах (параметрах) или их долях. Символ плоскости - (hkl). Системы координатных осей выбирают в зависимости от вида сингонии. Общими правилами являются: координатные оси параллельны ребрам

4 6

ячейки в должны быть связаны с имеющимися элементами симметрии.

Бели плоскость отсекает отрицательный отрезок на оси, то над со-ответствующим индексом ставится знак "минус".

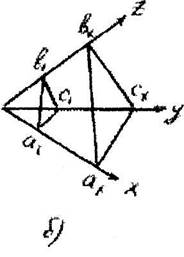
Например, (321). Если плоскость параллельна какой-либо коорди-натной оси, то соответствующий индекс равен нулю (отсекаемый отрезок равен со). Например, (110). Пример нахождения индексов плоскости по ве-личине отсекаемых отрезков дан рис.4.5.а.

Рнс. 4.5. К определению индексов плоскости (а) и грани (б)

Порядок нахождения индексов плоскости следующий:

1. Находим отрезки, отсекаемые плоскостью на координатных осях в
осевых единицах: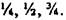

2. Берем обратные величины и находив их отношение: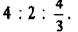

3. Приводим полученное отношение к отношению 3-х целых взаимно
простых чисел: 12:6:4=6:3:2.

4. Найденные числа заключаем в круглые скобки: (632) - символ
плоскости. Запятые ставятся в символе только после двузначного числа.
Например, (13, 10).

Если плоскость задана индексами (hkl), то это значит, что по оси X плоскость отсекает отрезок a/h, по оси Y - b/k, по оси Z - с/1.

У параллельной плоскости отсекаемые отрезки будут отличаться в целое число раз, одинаковое для всех 3-х осей. Это будет общий множи-тель на который можно сократить и символ плоскости не изменится.

Плоскости образующие куб называются плоскостями куба(рис 4.6.).

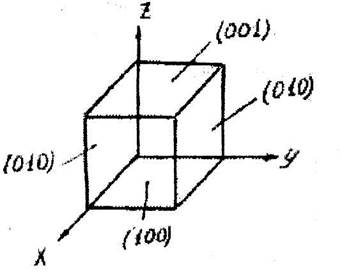
Рис. 4.6. Плоскости куба

(III) - плоскость кубического октаэдра. (ПО) -плоскость ромбического, до-декаэдра, т.к. система подобных плоскостей образует двенадцатигранник, каждая грань которого - ромб.

Как уже отмечалось ранее в гексагональной решетке используют 4-х осную систему координат (рис.4.7).

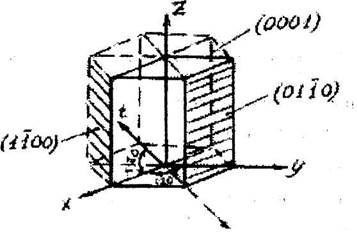
T

Рис. 4.7. Координатная система для гексагональной сингонии

Это вызвано тем неудобством, что в 3-х осной системе кристалло-
графически идентичные плоскости имеют разные индексы. Символ плос-
кости - (hkil). Третий индекс i, соответствующий горизонтальной оси t, не
является независимым, а определяется первыми двумя: i=-(h+k). В связи с
этим этим индексом иногда пренебрегают и в символ его место заменяется
точкой; (hk.l).;

Для охарактеризования расположения граней в кристалле выбирают в качестве масштабной единичную грань а₁, b₁, с₁, (рис.4.5,б). За коорди-натные оси принимают три непараллельных ребра кристалла. На основа-нии закона Гаюи находим индексы грани a_xb_xc_x:

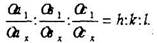
Как мы видели при рассмотрении базиса решетки кристалло­графические индексы узла это его координаты, выраженные в осевых единицах, записанные в двойных квадратных скобках [[u v w]].

Семейство кристаллографически идентичных направлений может быть охарактеризовано одним направлением -представителем семейства, проходящим через начало координат. В этом случае положение направле­ния в пространстве можно задать координатами любого узла, лежащего на заданном направлении.

Кристаллографические индексы направления - это 3 целых взаимно простых числа u, v, w, пропорциональных координатам любого узла, ле-жащего на этом направлении. Координаты измеряются в осевых единицах или их долях. Порядок нахождения индексов направления следующий.

1. Направление переносится параллельно самому себе в начало коор-
динат.

2. Находятся координаты ближайшего узла к началу координат.

3. Отношение найденных чисел приводится к отношению 3-х целых
взаимно простых чисел и записывается в квадратных скобках. Символ на-
правления - [u v w].

Индексы важнейших направлений в кубической решетке приведены на рис.4.8.

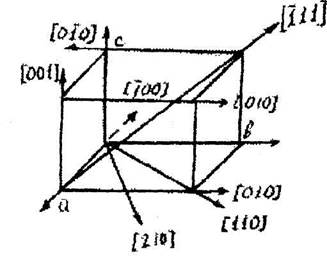
Рис. 4.8. Важнейшие направления в кубической решётке

Пусть, например, координаты узла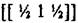

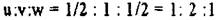. Искомое направление [121].

Рассмотрим основные кристаллографические соотношения.

Date: 2015-09-24; view: 624; Нарушение авторских прав