Модель международной торговли. (модель обмена)

Оптимальной моделью обмена является модель, которая позволяет торгующим между собой странам обеспечить взаимную выгоду. Для международной торговли это означает отсутствие значительного дефицита торгового баланса для каждой из стран.

Рассмотрим общий случай, когда торговлю между собой осуществляют n - стран, причем 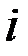-я страна выделяет на приобретение товаров, в том числе и внутри страны, сумму , составляющую ее бюджет.

Пусть 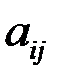– доля госбюджета, которую -я страна тратит на закупки товаров 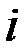-й страны. Тогда после подведения итогов торговли за год 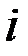-я страна получит выручку:

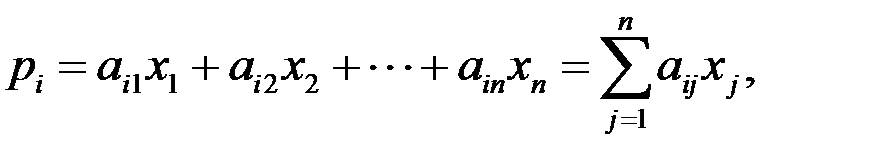
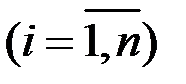(1.14)

или в векторно-матричной форме

p = Ax,

где А 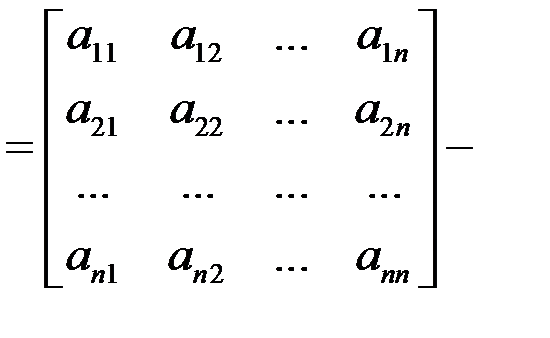матрица долей госбюджета, идущих на покупку товаров;

р 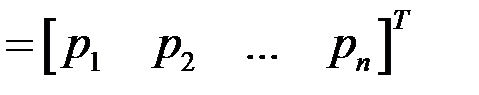– вектор-столбец выручек;

х – вектор-столбец бюджетов стран.

Заметим, что сумма элементов матрицы А в каждом столбце равна единице:

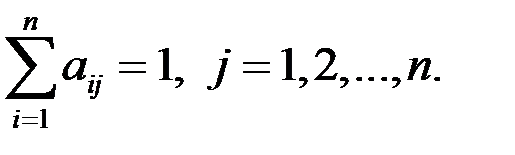(1.15)

Утверждение. Условием бездефицитной торговли является выполнение равенства:

р = х или Ах = х, то есть 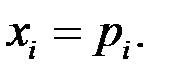(1.16)

Доказательство. Предположим,что для некоторого 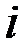-го государства справедливо неравенство 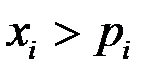(). Запишем условие (1.16) с учетом предположения:

;

;

……………………………………….

……………………………………….

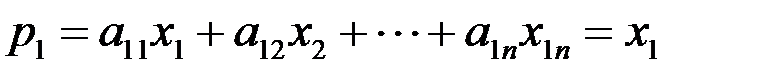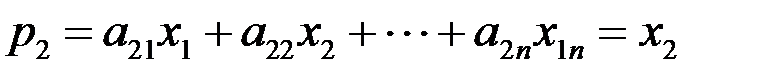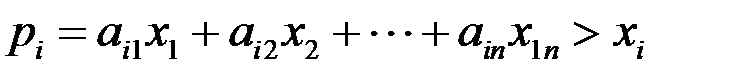
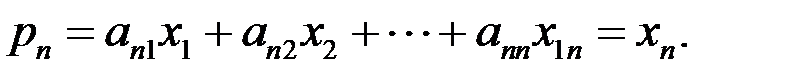
Сложив все равенства и одно неравенство, получим:

.

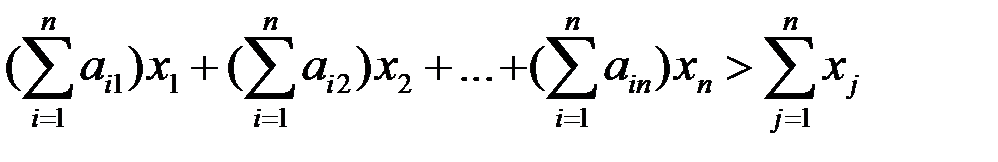Так как суммы в скобке в соответствии с (1.15) равны единице, то получим противоречивое неравенство:

.

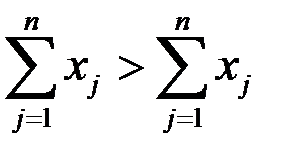Значит, наше предположение неверно. Аналогично в случае 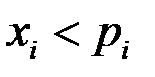получим: .

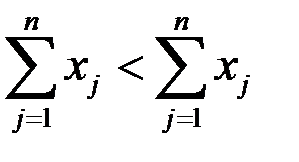Следовательно, доказательство завершено. Другими словами, условие сбалансированной (бездефицитной) торговли означает, что для каждой страны ее бюджет должен быть равен выручке от торговли.

Уравнение (1.16) означает, что собственный вектор структурной матрицы А, соответствующий собственному значению λ = 1, имеет своими компонентами бюджеты стран, осуществляющих бездефицитную международную торговлю.

Переписав уравнение (1.16) в виде

(А – Е) х = 0, (1.17)

получим уравнение, позволяющее определить вектор х соответствующий λ = 1.

Date: 2015-09-18; view: 614; Нарушение авторских прав