Продуктивные модели Леонтьева

Определение. Матрица A 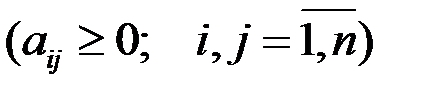называется продуктивной, если для любого вектора y 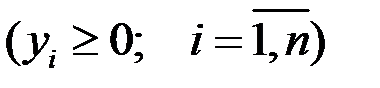существует вектор x 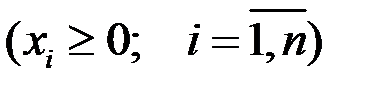, который является решением векторно-матричного уравнения:

x = Ax + y. (1.5)

Модель Леонтьева, у которой матрица A продуктивная, называется продуктивной моделью.

Рассмотрим две теоремы, устанавливающие критерии продуктивности.

Теорема 1. Первый критерий продуктивности.

Если для матрицы А 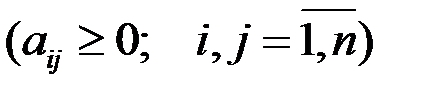и для некоторого вектора y 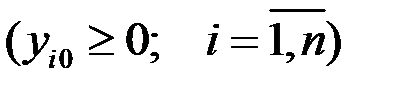уравнение (1.5) имеет решение x 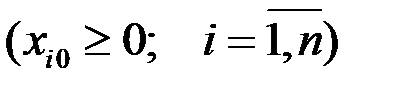, то матрица А продуктивна. без доказательства.

Данная теорема утверждает, что нет необходимости требовать существования решения x 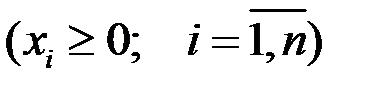уравнения (1.5) для любого вектора y 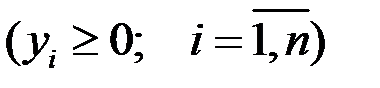, а достаточно найти хотя бы один такой вектор.

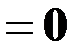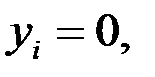
Для замкнутой экономической модели таким вектором может быть вектор y ( 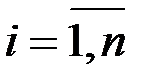). Тогда уравнение примет вид:

х = Ах или (А – Е) х = 0, (1.6)

где Е – единичная матрица.

В этом случае решение х является собственным вектором матрицы А, соответствующим её собственному числу 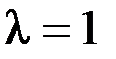. Таким образом, для продуктивности закрытой модели необходимо, чтобы матрица прямых затрат А имела собственное число .

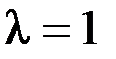Теорема 2. Второй критерий продуктивности.

Матрица А 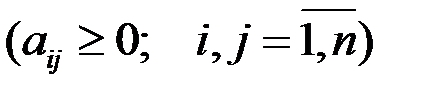продуктивна тогда и только тогда, когда матрица (Е – А)^–1 существует и неотрицательна.

Доказательство. Запишем уравнение Леонтьева (1.5) в виде

x – Ax = y, или (А – Е) х = y. (1.7)

Доказательство необходимости. Матрица С = (Е – А)^–1 существует и 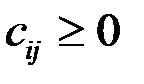. Тогда решение

x = (Е – А)^–1 y (1.8)

существует, а поскольку у вектора y все компоненты 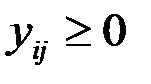, то и у вектора x все компоненты больше или равны нулю, т. е. 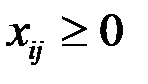. Следовательно, матрица А продуктивна.

Доказательство достаточности. Матрица А продуктивна. Рассмотрим вектор

y 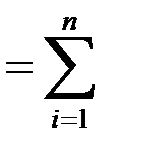е_i,

где е ₁ , е ₂ , …, е_n 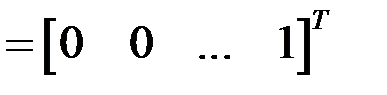–вектор-столбцы.

Тогда, поскольку система уравнений (1.5) линейна, можно рассмотреть эквивалентную ей систему из n линейных систем уравнений:

(Е – А) x = е ₁,..., (Е – А) x = е_n.

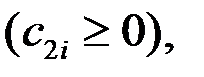Каждая из этих систем в силу продуктивности матрицы А имеет неотрицательное решение с ₁ с ₂ …, с_n 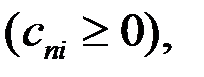то есть

(Е – А) с ₁ = е ₁, (Е – А) с ₂ = е ₂, …, (Е – А) с_n = е_n.

Обозначим через с матрицу, столбцы которой являются вектор-столбцами, то есть С = [ c ₁, с ₂, …, с_n ].

Так как E = [ e ₁, e ₂, …, e_n ] является единичной матрицей, то (Е – А) C = E, следовательно, матрица C есть обратная матрица (Е – А)^–1 к матрице (Е – А), причём 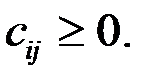Теорема доказана.

Замечание 1. Экономический смысл вектора е_i означает, что на внешнее потребление выпускается только одна единица продукта i- й отрасли, так как

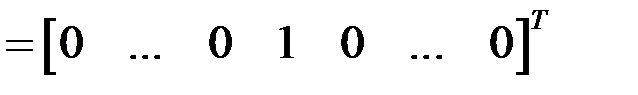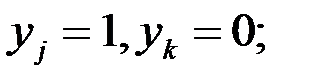y = или k 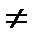j, k = .

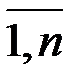Замечание 2. согласно замечанию 1 имеем

х = Се_j 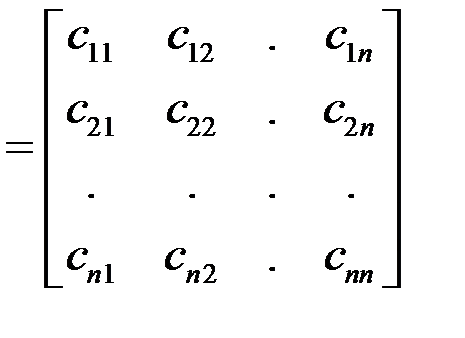= = 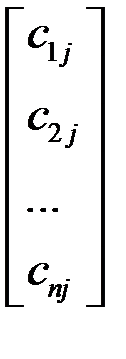с_j. (1.9)

Тогда 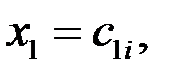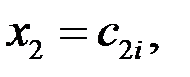…, 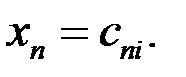В отличие от матрицы А, характеризующей прямые затраты на выпуск валового продукта, матрица С характеризует затраты на выпуск товарного продукта. Поэтому матрицу С называют матрицей полных затрат. Можно показать, что .

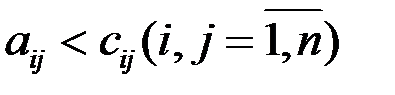Пример. Исследовать на продуктивность матрицу A и вычислить план х, если

y^T = [50,100], A = .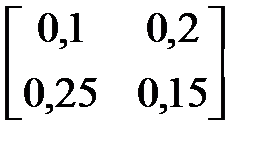

Решение:

E – A = 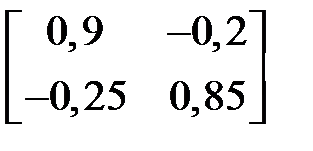, (E – A)^–1= C = .

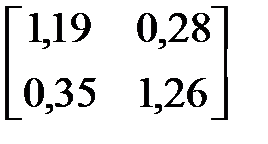Из примера видно, что 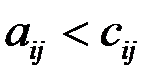. Тогда

x = Cy = .

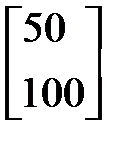
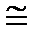
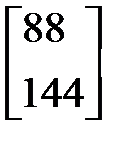Таким образом, необходимо произвести 88 и 144 единиц товара, чтобы обеспечить внепроизводственную сферу соответственно 50 и 100 единицами.

Date: 2015-09-18; view: 1598; Нарушение авторских прав