Модель равновесия цен

Кроме модели Леонтьева, существует двойственная ей, так называемая модель равновесных цен.

Обозначим через p^T 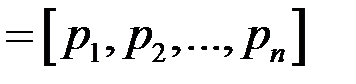транспонированный вектор-столбец цен, 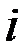-я координата которого 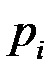равна цене единицы продукции 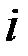-й отрасли; x^T 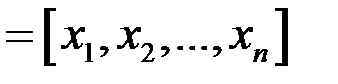– транспонированный вектор-столбец валового выпуска x; A – матрицу прямых затрат.

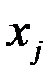Как и ранее, предполагается, что каждая отрасль производит один вид продукта (изделия). Тогда, если -я отрасль выпускает единиц изделий, то она получит доход, равный _. Часть своего дохода, а именно

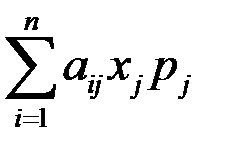
-я отрасль вынуждена будет потратить на закупку изделий других отраслей. Оставшуюся часть обозначим через 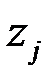. Эта часть дохода идёт на предпринимательскую прибыль и инвестиции, на выплату налогов и зарплат и т. д. Она носит название добавленной стоимости.

С учётом названных доходов и расходов уравнение баланса, выраженное в денежных единицах, примет вид:

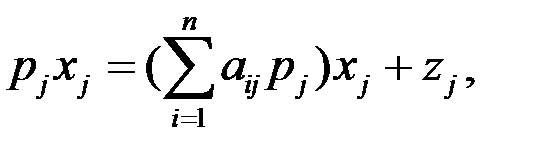(j = 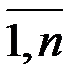). (1.10)

После деления на 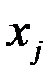всех членов соотношения (1.10) оно запишется в следующей форме:

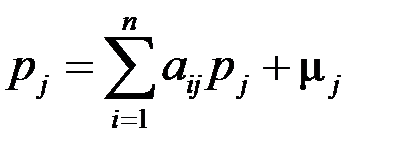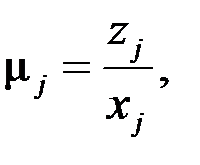, где (j = 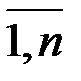). (1.11)

Величина 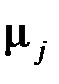, равная отношению добавленной стоимости 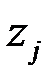к сумме единиц выпускаемой продукции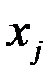 -ой отраслью, называется нормой добавленной стоимости.

Систему n скалярных уравнений (1.11) можно записать в векторно-матричной форме:

p = A^Tp + m, (1.12)

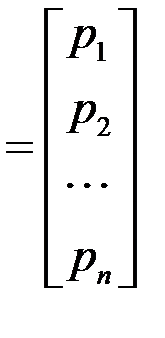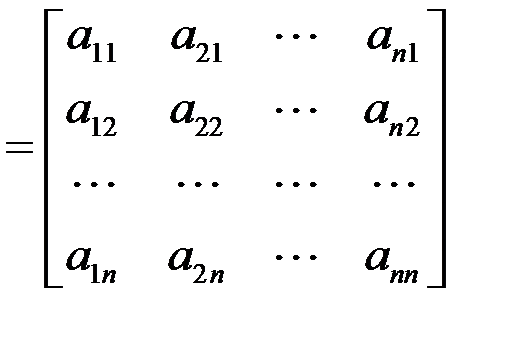где p , A^T , m = .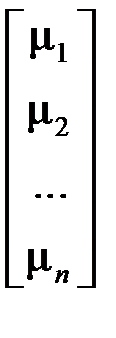

Уравнение (1.12), являющееся моделью равновесных цен, имеет внешнее сходство с моделью Леонтьева (1.5). Отличие заключается в замене вектора валового выпуска x на вектор стоимости p, вектора конечного потребления y на вектор норм добавленной стоимости m, а матрица A заменена на транспонированную матрицу A^T.

Модель (1.12) позволяет прогнозировать цены на продукцию отраслей, изменение цен и инфляцию, зная нормы добавленной стоимости. Для этого необходимо соотношение (1.12) преобразовать:

Ep – A^Tp = m, или (E – A^T)p = m.

Отсюда

p = С^T m, где С^T = (E – A^T) ^{– 1}. (1.13)

Пример. Для производства железнодорожных вагонов используются ресурсы топливно-энергетической отрасли, машиностроительной и лесной промышленностей.

Пусть A^T 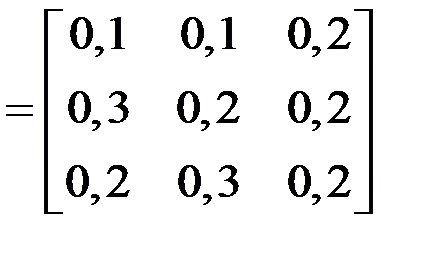– транспонированная матрица прямых затрат на производство единицы продукции отмеченных отраслей, m 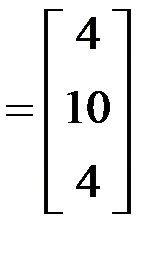– вектор норм добавленной стоимости на единицу продукции соответственно топливно-энергетической, машиностроительной и лесной отраслей.

Необходимо определить равновесные цены продукции и изменение цен в случае увеличения нормы добавленной стоимости топливно-энергетической отрасли с 4 до 5,45 единиц.

Решение

Для определения равновесных цен воспользуемся формулой равновесных цен (1.13):

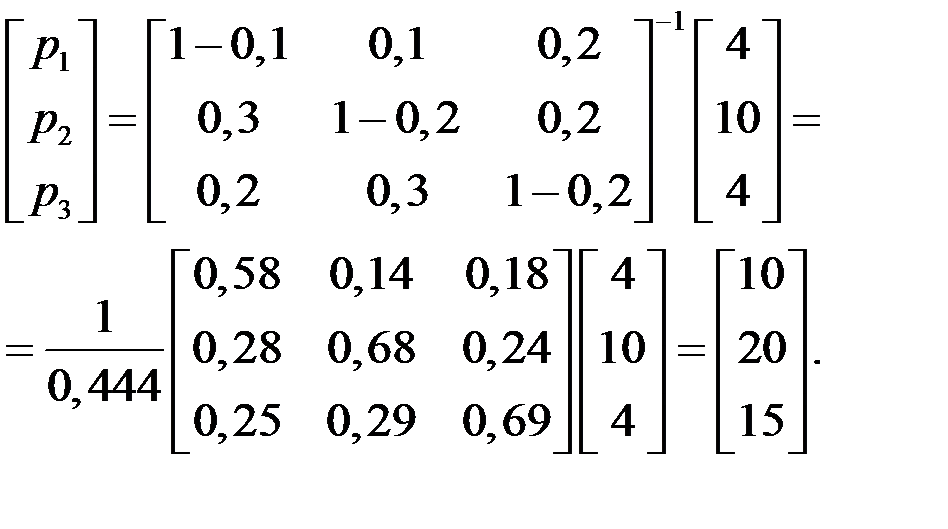
В случае изменения нормы добавленной стоимости будем иметь:

,

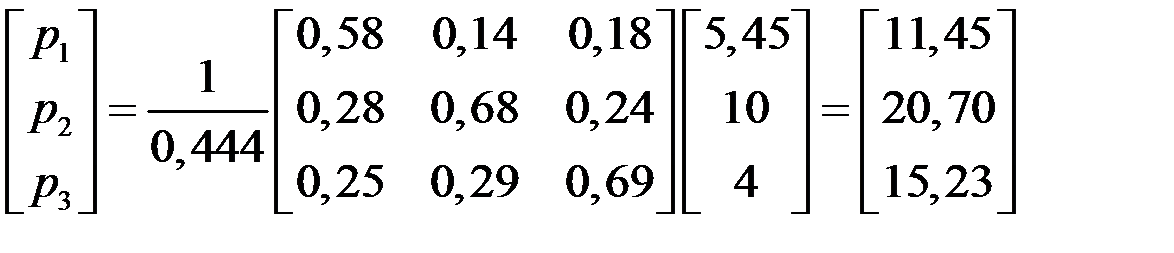то есть продукция первой отрасли подорожала на 14,5 %, второй – на 3,5 %, третьей – на 4,17 %.

Date: 2015-09-18; view: 570; Нарушение авторских прав