Ошибки возникающие при регрессионном анализе

Регрессионный анализ – это раздел математической статистики, изучающий зависимость между случайными величинами с помощью уравнений регрессии (функций регрессии).

теоретически возможны две регрессии: одна единственная для генеральной совокупности и вторая, зависящая от выборки. Последнюю регрессию называют выборочной, или эмпирической функцией регрессии, а ее график в системе координат 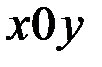– линией регрессии. Коэффициенты α и β линейной зависимости (2.2) для генеральной совокупности определить невозможно, так как обычно генеральная совокупность неизвестна. 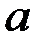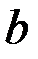Коэффициенты выборочной линейной регрессии (1.4) и являются выборочными коэффициентами или оценками параметров α и β. Выборочные линии регрессии для различных выборок имеют разный наклон (коэффициент 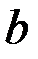) и разные точки пересечения с осью 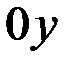(коэффициент ).

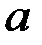Следует заметить, что при положительном наклоне генеральной регрессии наклон выборочной линии регрессии может оказаться для некоторых выборок отрицательным или отсутствовать. Однако это не будет свидетельствовать об отсутствии или отрицательной связи исследуемых переменных. Для того, чтобы убедиться, что получена качественная связь показателей экономического процесса, необходимо помимо оценки коэффициентов регрессии находить их стандартные отклонения и t -статистики. С помощью их можно судить о статистической значимости построенной математической модели.

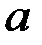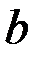Для получения оценок и значений параметров линейной зависимости α и β используется метод наименьших квадратов (МНК). Метод в качестве критерия близости значений теоретических и опытных данных использует минимум суммы квадратов разностей наблюдаемого и рассчитанного по уравнению регрессии показателя результата. Другими словами, критерием оценивания коэффициентов служит минимум суммы наблюдаемых случайных отклонений для данного линейного уравнения регрессии.

При использовании метода наименьших квадратов необходимо, чтобы выполнялись следующие требования (условия Гаусса–Маркова) по отношению к случайным теоретическим ошибкам:

1) значения переменной 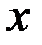являются величинами неслучайными (детерминированными);

2) математическое ожидание ошибки 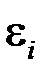равно нулю, то есть ;

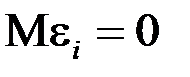3) дисперсия ошибки 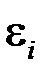равна постоянной величине, то есть ;

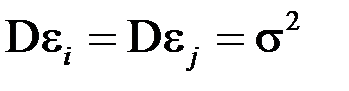4) ошибка 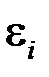является случайной величиной, распределенной по нормальному закону;

5) значения ошибок 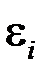попарно независимы, следовательно:

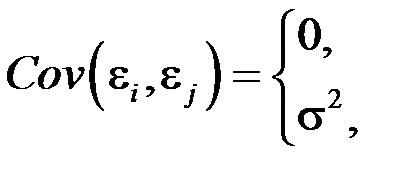
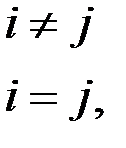
то есть для них характерна некоррелированность.

Условие 3 известно как свойство гомоскедастичности. Невыполнение этого условия приводит к свойству гетероскедастичности.

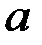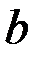Известно, что если условия 1–5 выполняются, то оценки и метода наименьших квадратов обладают рядом свойств.

Во-первых, оценки являются несмещенными, то есть математическое ожидание оценки каждого параметра равно его истинному значению: 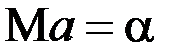; 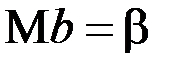. Это обусловлено тем, что 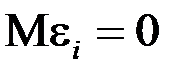и свидетельствует об отсутствии систематической ошибки в определении положения линии регрессии.

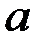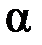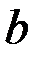Во-вторых, оценки состоятельны, так как дисперсия оценок параметров при увеличении числа опытных данных в методе наименьших квадратов стремится к нулю. Другими словами, если число опытов достаточно велико, то практически близко к , а к 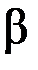, следовательно, надежность оценки при увеличении выборки растет.

В-третьих, оценки эффективны, то есть они имеют наименьшую дисперсию по сравнению с любыми другими оценками данного параметра.

Перечисленные свойства не зависят от вида распределения случайной ошибки, тем не менее обычно предполагается, что они имеют нормальный закон распределения. Эта предпосылка позволяет проводить проверку статистической значимости оценок метода наименьших квадратов и определения для них доверительных интервалов. При ее выполнении оценки МНК имеют минимальную дисперсию не только среди линейных, но и среди несмещенных оценок.

Если требования 3 и 4 не выполнены, то есть дисперсия теоретических ошибок непостоянна или их значения связаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности отсутствует.

Наиболее важным является выполнение требования 5, которое в случае его невыполнения приводит к нарушению свойства несмещенности.

Поскольку данные о случайных теоретических отклонениях от линейной зависимости обычно отсутствуют, то для исследования статистического качества оцененного уравнения регрессии необходимо провести следующие проверки:

– статистической значимости каждого коэффициента уравнения регрессии;

– общего качества уравнения регрессии;

– свойств данных, выполнение которых предполагалось при оценивании уравнения регрессии.

29.Прямая лин.регрессия (парная лин.регр) - это причинная модель статист. лин.связи м/у двумя колич-ными переменными х и у, предст-ная уравнением y = a + bx, где х – незав.переменная, y –зависимая.Коэф-т регрессии- b и свободный член ур-ния регрессии- a вычисляются по формулам:b = r_xySy/Sx; a = y - bx,

Пусть 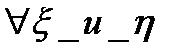, кот.заданы своей выборкой 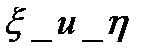. Х=[х1,х2...хn] Y= [y1,y2..yn] (столбцы).

Будем рассм. парную связь в кот.: 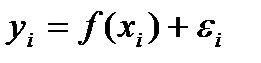все др.факторы приводят к некоторым отклонениям опытного зн-я от теорет. 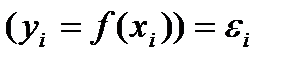Будем отклонения называть- случ. теорет. отклонениями (ошиб.). В кач-ве ф-ции f(x) будем принимать ф-ю регрессии, те. ф-ю условное математ.ожидание: f(x_i)= М(y_i|x_i). Чаще всего в кач-ве усл. матем.ожид.приним. линейную ф-ю: М(y_i|x_i)=а+bx_iày_i= а+bx_i+ 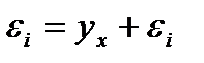, где 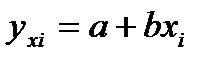. 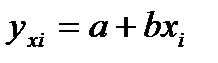- для любой (.) (*)-лин.парная регрессия. Для построения (*) необход.по опытным данным найти коэф. а,b, где b- коэф.регрессии. Схема –кореляц.поле. На него можно нанести бесконечное мн-во прямых, каждый из кот.будет характеризовать а,b. Необходимо найти "наилучшую" прямую, т.е ту кот. в сумме имеет наименьшее отклонение. Метод нахожд. называется- "МНК".

30.Анализ коэф.корелляции и детерминации. После того как найдена ф-я регрессии производится оценка значимости как ур-я регрессии так и так коэф. Оценка значимости ур-я регрессии в целом производ.с помощью Fкр Фишера. Провести с помощью коэф. корелляции.- Коэф.корел. - показатель тесноты связи (лин.) м/у результативн. признаком и фактором. Согласно опред.корел.,он для генеральн.совокупности их двух случ.велечин 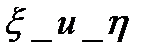à из Т.вероятности: 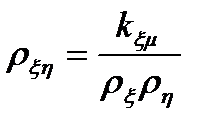(*), но на практике – коэф. корел. опред. по выборке. – Выборочный коэф.-( приближ.зн-е) оценка коэф.корел.генер.совокупности. r_xy-оценка выборки (*). 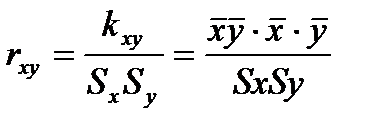; 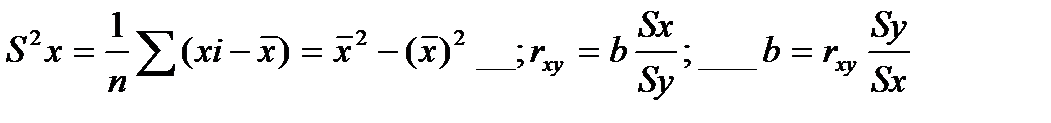. (-1< r <1) при b>0 0<r< 1, при b<0 -1<r< 0.

- Коэф.детерминации -характериз.долю (разброс) дисперсии результатив. признака ^yi, кот.объясняется лин.регрессией.

М/у коэф.коррел.и детермин. для лин.ф-ии существ.связь.Можно показать: r = r² _xy (коэф.детермин.=коэф.корелл.в кв.)

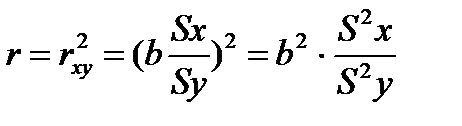. Для Нелин. регрессии:- индекс коррел.Rxy; - индекс детерминации R²_xy

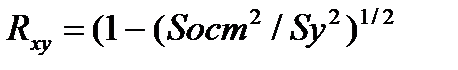
31.Дисперсионный анализ лин. регрессии.

Основной целью дисперсионного анализа является исследование значимости различия между средними.

Центральное место в дисп.анализе занимает разложение общей суммы кв.отклонений результирующего показателя у от его сред.зн-я у (с чертой) на две части: объясненную и остаточную.

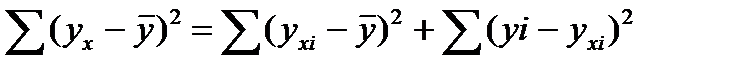Результаты расчетов сводим в табл.

Непосредственному определению коэффициента детерминации предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений результирующего показателя у от его среднего значения 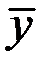на две части: на объясненную (факторную) функцией регрессии и необъясненную (остаточную).

Тогда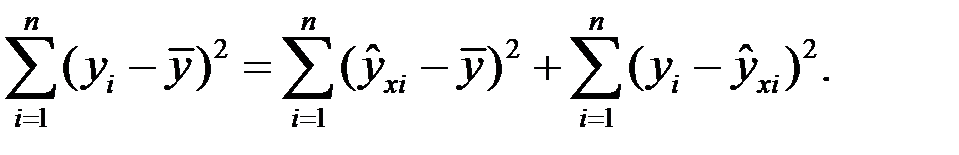

Таким образом, условно все факторы, определяющие изменение результирующего показателя, разделены на две группы: изучаемый фактор x и прочие факторы. Если изучаемый фактор x не оказывает влияния, то линия регрессии параллельна оси 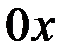, т. е. уравнение регрессии будет иметь вид: .

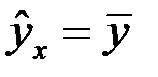В этом случае влияние оказывают другие факторы, и, следовательно, вся дисперсия результативного признака обусловлена другими факторами.

Если другие факторы не оказывают влияние на результат 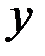, то он связан с фактором 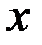функционально, и сумма квадратов остатков будет равна нулю. В этом случае все точки корреляционного поля будут лежать на корреляционной прямой.

Таким образом, если сумма 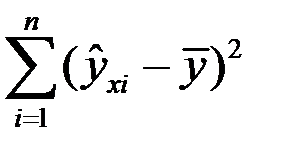значительно превышает сумму 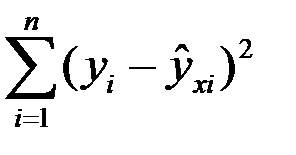, то уравнение регрессии значимо.

33.Оценка существ-ти пар-ров лен. рег-ии. Параметры линейной регрессии (коэффициент регрессии 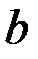и свободный член 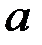) являются случайными величинами, поскольку они вычислены с помощью элементов выборки, которые в свою очередь являются тоже случайными величинами. Математические ожидания параметроврегрессии, в предположении выполнения условий Гаусса–Маркова, соответственно равны параметрам регрессии соответствующей генеральной совокупности, а именно: 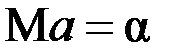и

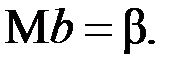
При этом оценки тем надежней, чем меньше их разброс, то есть дисперсия: 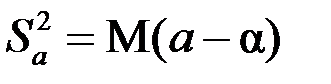и 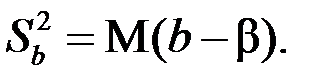Надежность получаемых оценок a и b зависит от дисперсии случайных отклонений 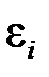,которые неизвестны, а поэтому заменяются при анализе надежности параметров регрессии на дисперсию отклонений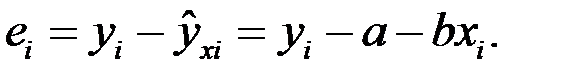

В математической статистике доказано, что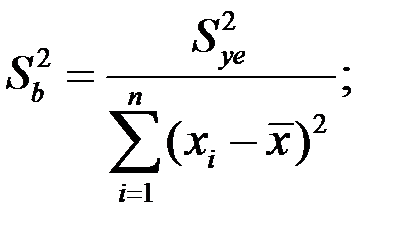

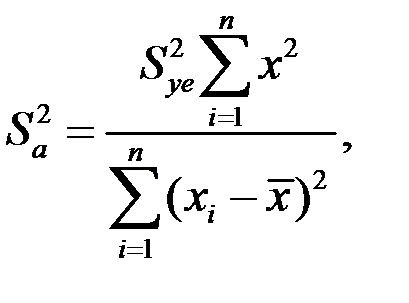где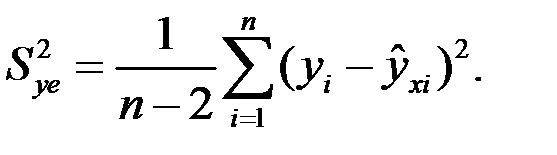

Здесь 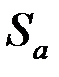и 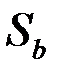– стандартные отклонения (среднеквадратичные отклонения) случайных величин 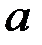и 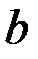. Приведенные соотношения можно дополнить следующими пояснениями. Коэффициент 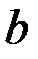есть мера наклона линии регрессии. Тогда, чем больше разброс значений результирующего показателя y вокруг линии регрессии, тем больше ошибка в определении наклона линии регрессии. В знаменателе формулы для 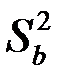стоит сумма квадратов отклонений фактора от среднего его значения. Эта сумма велика в том случае, если регрессия построена на достаточно широком диапазоне значений фактора. Тогда при данном разбросе результирующего показателя ошибка в оценке величины наклона прямой будет меньше. То же самое при большом числе наблюдений 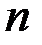. Что касается свободного члена уравнения регрессии 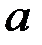, то его выборочная дисперсия пропорциональна дисперсии коэффициента регрессии 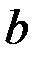. Следовательно, чем больше ошибка в определении коэффициента регрессии, тем больше разброс свободного члена.

Статистическая значимость оцененного коэффициента регрессии 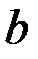может быть установлена с помощью анализа его отношения к своему стандартному отклонению. Эта величина, в случае удовлетворения условиям Гаусса–Маркова, имеет t -распределение Стьюдента с 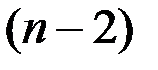степенями свободы. Она носит название t -статистики: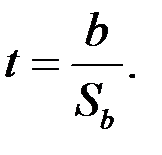

Таким образом, величина стандартной ошибки совместно с t -распределением Стьюдента при 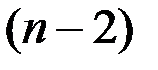степенями свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительных интервалов при интервальном оценивании.

Для t -статистики проверяется нулевая гипотеза 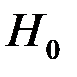о равенстве нулю статистики. Легко видеть, что при 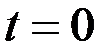однозначно 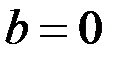. При проверке значимости коэффициента регрессии определяется фактическое значение t -критерия Стьюдента 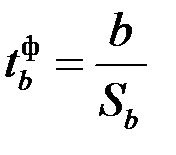, которое затем сравнивается с табличным значением. Процедура проверки коэффициента регрессии 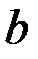и свободного члена a уравнения регрессии аналогична, как с помощью F -статистики производилась проверка значимости уравнения регрессии, которая приведена в разделе 2.6.

Следует заметить, что значение t -критерия Стьюдента можно вычислить также, извлекая корень из F -критерия, т. к. 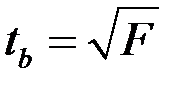. Действительно,

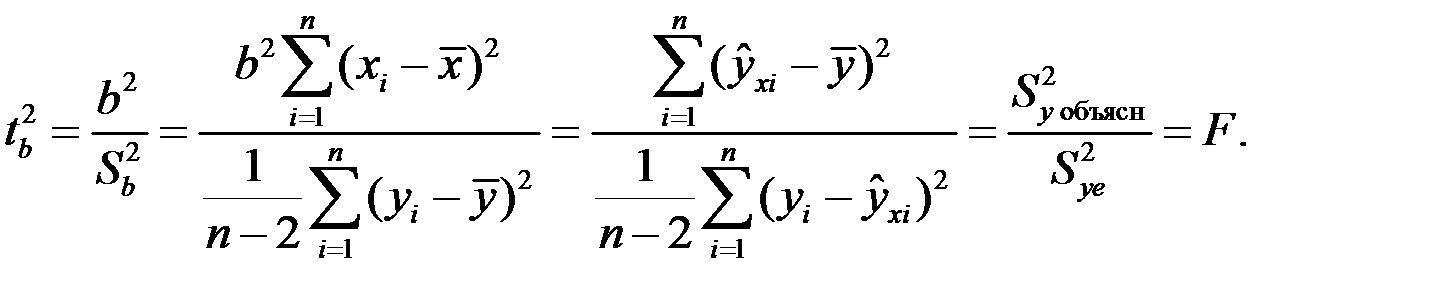
34.Оценка значимости линейной регрессии. Осущ-ся с помощью F-критерия Фишера,котор. сопоставляет факторную(объясненную) и остаточную дисперсии в расчете на одну степень свободы.Для вычисления F- критерия Фишера используется разложение общей суммы квадратов отклонений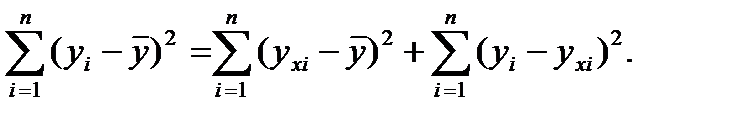

Сравнение 2-х сумм квадратов отклонения позвол.вып-ть оценку значимости ур-я рег-ии.Устан-м число степеней своб. для кажд. суммы квадратов отклонений При этом число степеней свободы-число единиц совокупности выборки и число определяемых констант.Для общей суммы 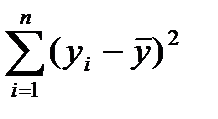одно значение вычисл. через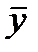 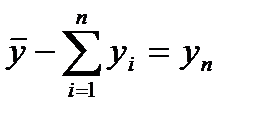,число степ. своб. =(n-1).Тогда 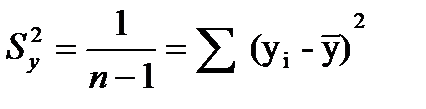-выборочная общая дисперсия.При опр-ии числа степ. своб. для факторной суммы квадратов 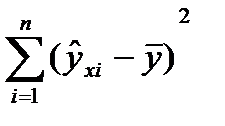исп-ся выраж. 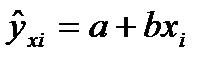, число b хар-ет степень свободы. Тогда для остат-й суммы квадр. число степ. своб. = n-2.Знач. дан. сумма имеет одну степ. своб. и тогда: =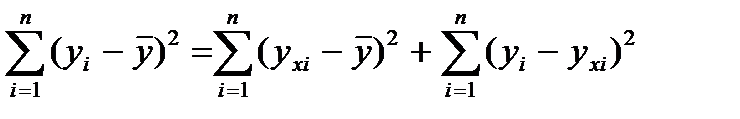

,

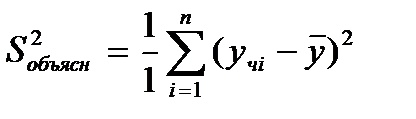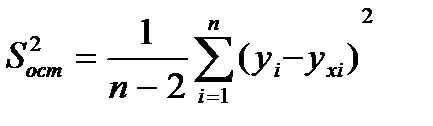
Приведен. соотнош. дают возмож. исп-ть их для оценки стат. значим-ти ур-я рег-ии., кот. вкл. след. этапы: (для оцен. знач. выдвиг. след. гипотезы)

1) 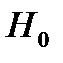,кот. утвержд. что факторн. сумма на 1-ну степ. своб. = остат.; и выдвиг альтернатив. гипот. 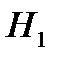,в кот. говор-ся что эти суммы не равны.2)В кач-ве критерия примен. стат-ка представл-я собой отнош-е: 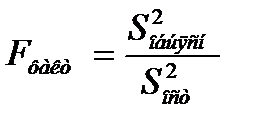Предполог. при справедлив. гип-зе 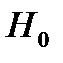отнош-е F распределено по закону ФЫишера (F распр-е) к1=1,к2=n-2; Fтабл (к1,к2)-закон Фишера(привод в табл);3)Выбирается Ур-нь знач-ти α,кот. обыч приним 0,05; 0,1.4)По табл. Фиш. нах-ся знач F по заданному уровню α; 5)Сравнив-ся таблич знач и вычисл-е знач. F-крит. Фиш. Если Fфакр<Fтабл, то вероят-ть 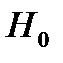выше заданного Ур-ня α.И она не м.б. отклонена без существенного риска соверш. неправ. выбор о наличии связи м/у результат-м показат. и фактором. В этом случае Ур. рег. след. полог. незначимым. В против. случ. нулевая гипот. отверг. и приним альтернатив., и счит. Ур. рег. качественным(Fфакр<Fтабл)

35.Прогноз по линейн. ур. рег-ии. Точечный расчет результир-й переем-й 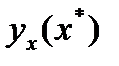д.б. дополнен расчет. стандарт. ошибки 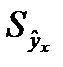. Для вывода формулы определения вел. станд. ошиб. результир-й пер-й 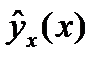рассмотр. Ур-елин. рег.: 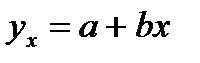,подставив в него знач. для коэф. а получим 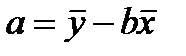, 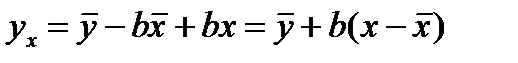Выбороч. диспер. (квадрат станд. ошибки) 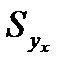результ. переем. 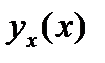завис. от ошиибки 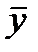и ошиб. коэф. рег. b, т.е.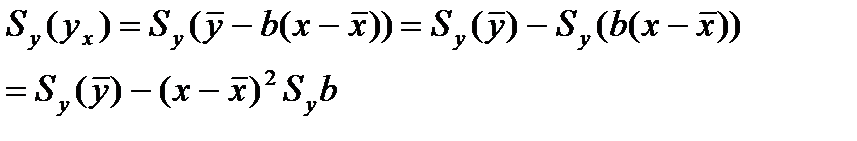

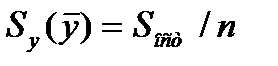
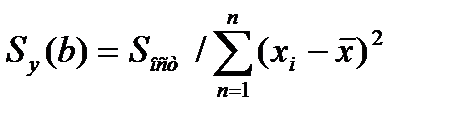-ошиб. коэф. рег.

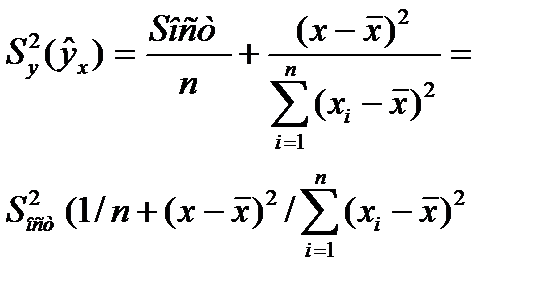
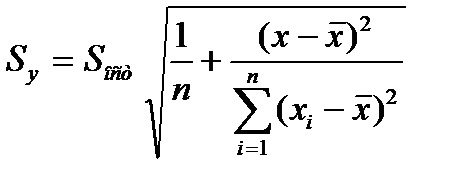
получ. форм. для стандарт. ошиб. результир. переем-й 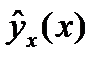при зад-х знач-ях х хар-ет ошибку положения лин. рег.Вел станд-й ошибки будет мин-й при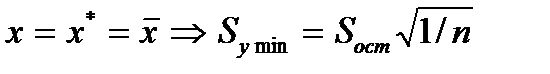

По мере удалания от 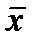Ош-ка возраст.. Т.е. чем > разность м/у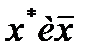 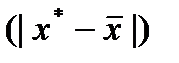тем > ош-ка.Поэт. след. иметь ввиду знач. результир. показ.След-т осущ-ть прогноз для х, кот. не слишком далеко расположены друг от друга.Фактич. знач. результир. фактора варьируется у вычисл-го 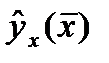.Индивид-е знач. м.б. отклон. от этого знач. на вел-ну, кот. опр-ся 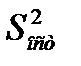и тогда формула буд. иметь вид: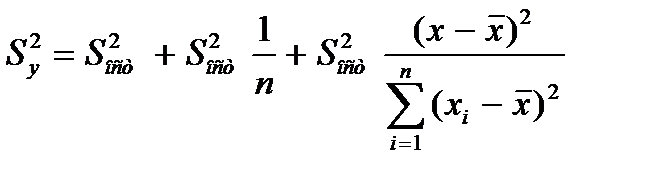

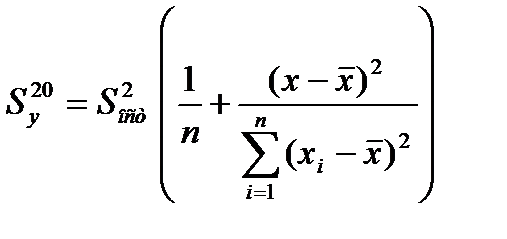
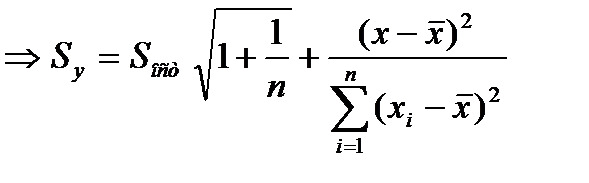
36.Оценка пар-в Нелин. рег. ,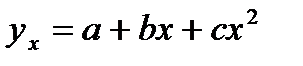

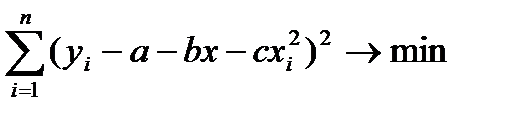
В этом случ. Нелин. ф-я м.б. исп-на, как линейная,как многочлен, коэф-т L (a,b,c)зависит от 3 перем-х т L (a,b,c)=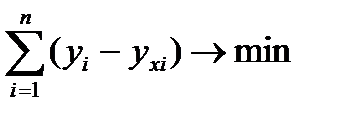

Сумма отклон. опытного и теоретич. д.б. миним-й.

Находим производные, затем используем метод Крамера.

37.Оценка параметров показат. регресс.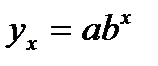

Для ее построен. (нахождения а и b)необх. в нач. произвести линеаризацию, а именно перейти от веществ. чисел xi и yi к их логарифмам.

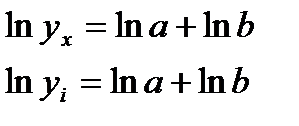
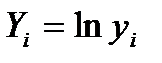
А=lna, B=lnb,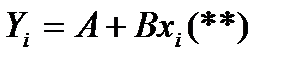

Примен. мет. наим. квадр. к ф-ии (**)

,

,

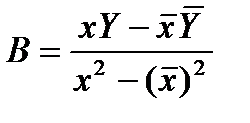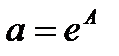
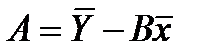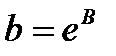
38.Оценка парам-в степенной рег-ии.

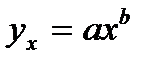, Для ее построен.(нахождения а и b)необх. в нач. произвести линеаризацию.

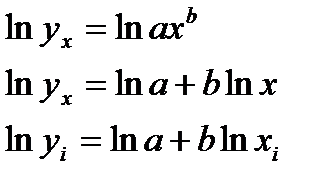
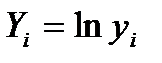
А=lna,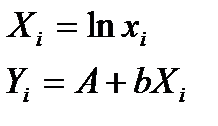

примен. мет. наим. квадр.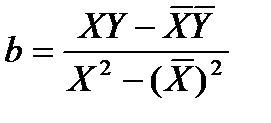

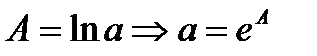
Найдя а и b окончательно запис-ся степенная ф-ия рег-ии.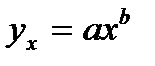

39.Индекс детерминации нелин. рег. Нелин. рег. хар-ся индексом корреляции 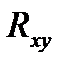и детерминации :

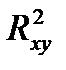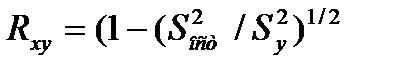
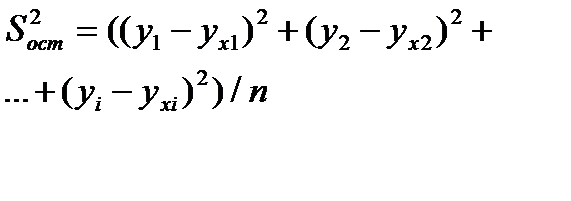
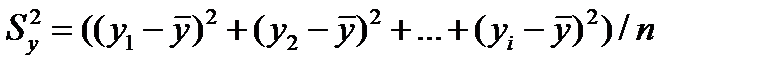
Величина дан. показателя нах-ся в пределах 0<= 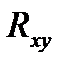<=1, чем ближе она к 1, тем теснее связь, тем более надежное Ур-е рег.

40,Индекс корреляц нелин.регрессии.

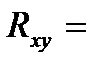(1-(Sост^2/Sу^2))^1/2

Sост^2= 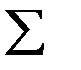(yi-yxi)^2 / n

Sу^2 = 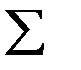(yi-yср)^2 / n

0<=Rxy<=1, чем ближе к 1, тем теснее связь между функцией и аргументом, тем более надежное уравнение регрессии.

41. Кривые Филипса - равносторонняя гипербола, характеризующая нелинейную зависимость междунормой безработици х и процентом прироста з/п у: у=а+b/х

42, Кривая Эйнгеля. Нем.статистик сформулир. В 1857г. закономерность, согласно кот. С ростом дохода доля его, расходуемая на непродовольственные товары, будет возрастать. Это увеличение имеет предел, поскольку сумма двух долей не может быть больше 100%, т.е. на отдельные непродовольств.товары этот предел может харак-ся величиной параметра а для уравнения вида: у=а-b/х.

43. Средняя ошибка аппроксим.

Фактическое значение результативного признака отличается от теоретического, рассчитанного по уравнению регрессии. Чем меньше это отличие, тем ближе теоретическое значение приближается к опытным данным, тем лучше качество математической модели регрессии для данной выборки. Поскольку как опытные данные, так и теоретические могут быть величинами как положительными, так и отрицательными, то при сравнении разности между ними 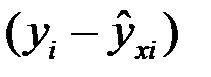следует рассматривать модуль этой разности 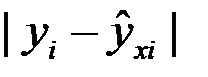. Эта величина характеризует аппроксимацию опытных данных, причем локальную, т. е. при конкретном 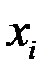. Сама величина не характеризует в полной мере качество аппроксимации, поэтому дополнительно вводится относительное значение модуля разности по формуле: 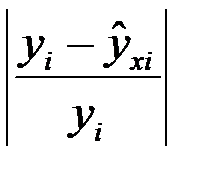. Данные величины можно рассматривать как абсолютную и относительную ошибки аппроксимации.

Обычно, особенно в экономике, относительную ошибку аппроксимации выражают в %:

.

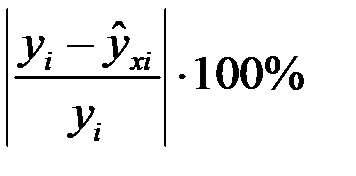Кроме локальной характеристики аппроксимации результирующего показателя в эконометрике вводится глобальная характеристика качества аппроксимации, под которой понимается средняя ошибка аппроксимации.

Если обозначить через A _i точечную (локальную) ошибку аппроксимации:

,

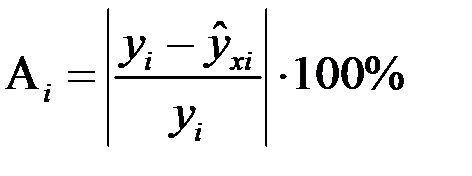то интегральная характеристика аппроксимации А и среднее значение 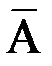будут вычисляться соответственно по формулам:

; .

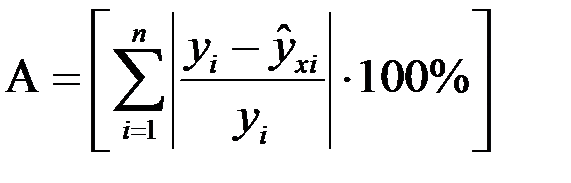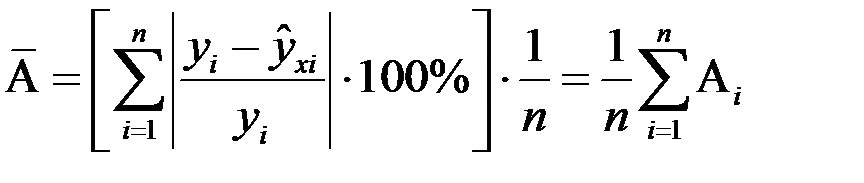Date: 2015-09-18; view: 3091; Нарушение авторских прав