Метод наименьших квадратов для построения производственных функций по опытным данным

С помощью метода наименьших квадратов в экономике оцениваются функциональные аналитические зависимости по опытным данным. Например, необходимо построить производственную функцию ОАО «РЖД», т.е. установить зависимости приведенной работы (грузооборота) железной дороги 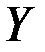от капитала 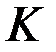и труда 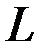. При этом известны опытные значения приведенной работы (млн. т-км), капитал (млн. руб.) и работа (чел.) для 17 железных дорог ОАО «РЖД» за несколько лет. Тогда производственная функция является функцией двух переменных – ресурсов.

Ресурсы, которые включаются в производственную модель, должны удовлетворять следующим требованиям:

– они должны быть количественно измеримы (для качественного фактора необходимо ввести количественный показатель);

– они не должны быть сильно внутренне связанными.

Аппроксимирующие функции нескольких переменных, как и для функции одной переменной, бывают линейные и нелинейные. Наиболее широко используются аппроксимирующие функции для 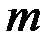переменных следующих типов:

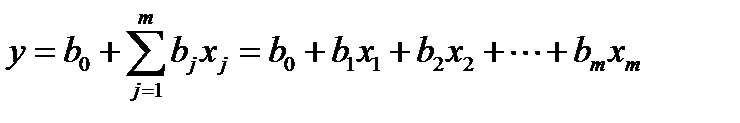- линейная аддитивная функция;

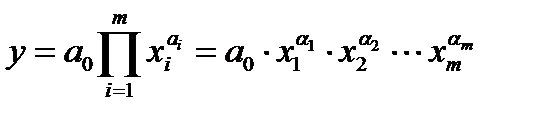- степенная мультипликативная функция.

Аналогично, как и для функции одной переменной [6], для функции нескольких переменных могут применяться и другие аналитические формы.

Как отмечалось, параметры (коэффициенты) линейной производственной функции определяются с помощью метода наименьших квадратов. При его применении строится система нормальных уравнений для оценки параметров производственной функции.

Рассмотрим эти уравнения применительно к линейной производственной функции вида:

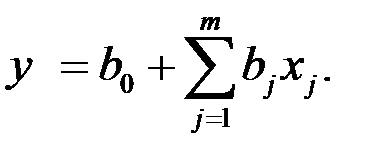
Для вычисления коэффициентов составляется функция, в качестве аргументов которой выступают искомые коэффициенты. Функция отражает сумму квадратов разностей опытных и теоретических значений производственной функции. Далее ставится условие достижения данной суммы минимального значения, т.е.

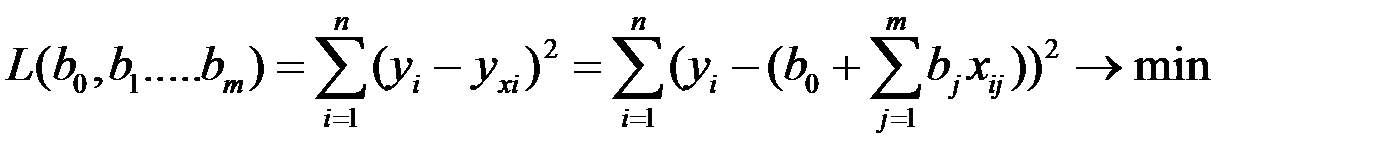
Для построения мультипликативной степенной производственной функции она приводится к линейной с помощью ее логарифмирования. Далее применяется метод наименьших квадратов.

17.Неоклассическая мультипликативная производств. ф-ция. Пр-ная ф-ция наз-ся неоклассической мультипликативной ф-цией, если она непрерывна и удет усл-ям:

1) F (0 ,L) = F(K,0) =0 - отсутствие одного из ресурсов не обеспечивает результата (продукта) производства;

2) 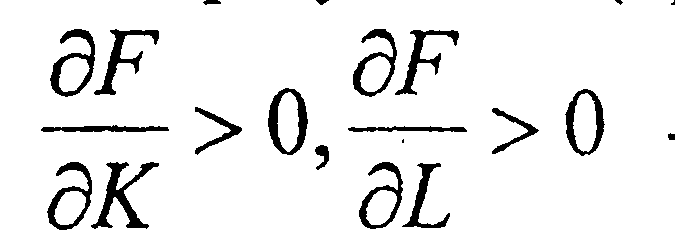- с ростом объемов ресурсов растет и объем

выпускаемого продукта;

3) 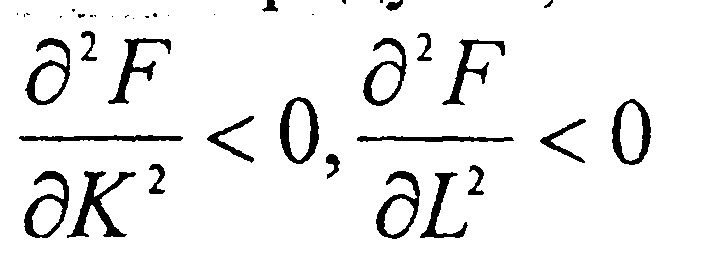- с ростом объемов ресурсов скорость роста

объема продукта снижается;

4) 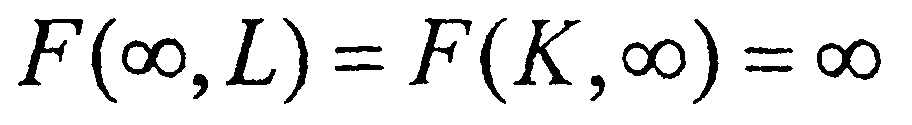- с неограниченным ростом объема одного из ресурсов выпуск продукта неограниченно растет.

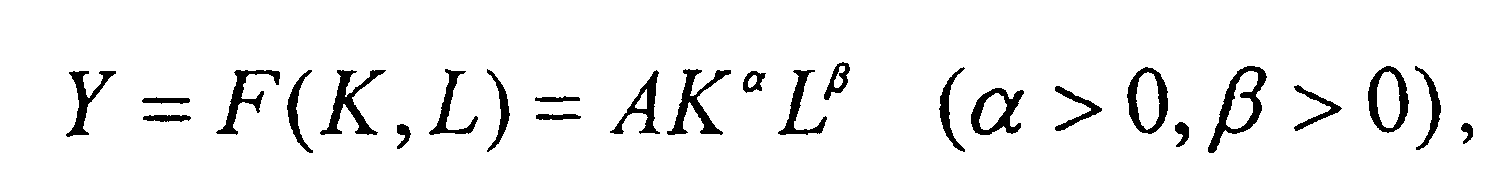Мультипликативная пр-ная ф-ция явл. степ. ф-цей и задается следующим аналит. выр-ем:

где А - коэффициент технического прогресса; α, β- пок-ли степени пр-ной ф-ции соответственно при ср-вах пр-ва и рабочей силе. Как отмечалось, в частном случае, когда 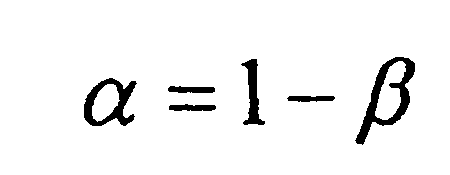мультипликатив. пр-ная ф-ция называется функцией Кобба - Дугласа.

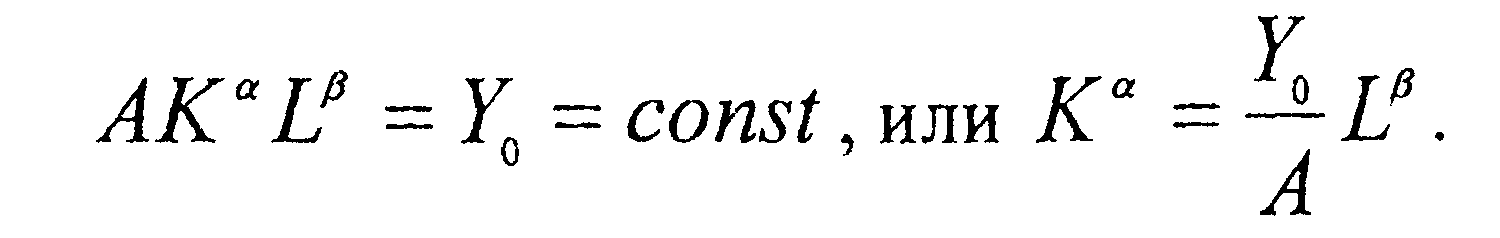18. Изокванты и изоклины мультипликатив. производств.ф-ции. Изоквантой, или линией уровня на плоскости KOL, наз-ся мн-во точек пл-ти, для кот. F(K,L) – Y₀ = const. Для мультипликативной пр-ной ф-ции изокванта имеет вид:

Она предст. степенную гиперболу, асимптотами которой являются оси координат ОК и OL. Для разных значений К и L, кот. формируют точку на конкретной изокванте, объем производимого продукта равняется значению Y₀. Так как на изокванте справедливо равенство 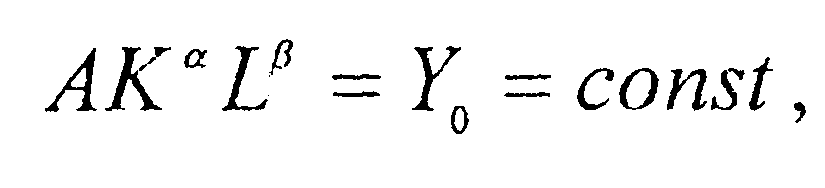, то диф-ал пр-ной ф-ции

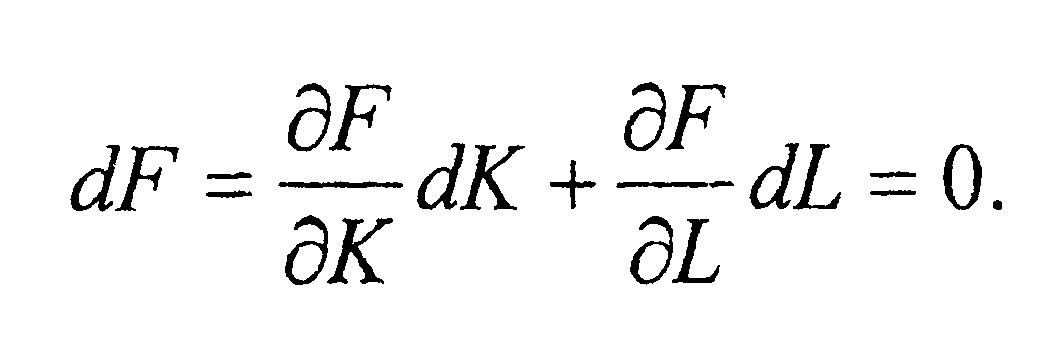
Изоклинами наз-ся линии на плоскости KOL наиболее быстрого роста пр-ной ф-ции. Изоклины ортогональны линиям нулевого роста, т.е. ортогональны изоквантам. Поскольку направления наиболее быстрого роста в каждой точке (K, L) задается градиентом

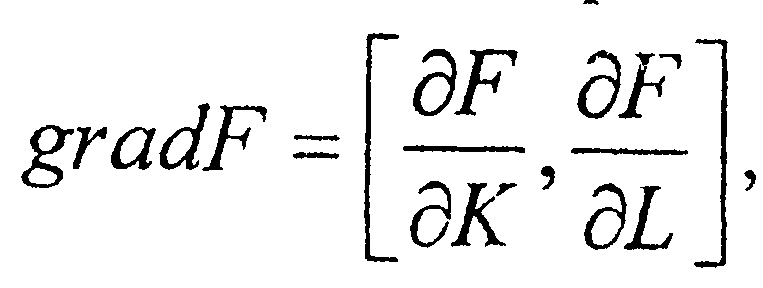, то уравнение изоклины можно записать

следующим образом:

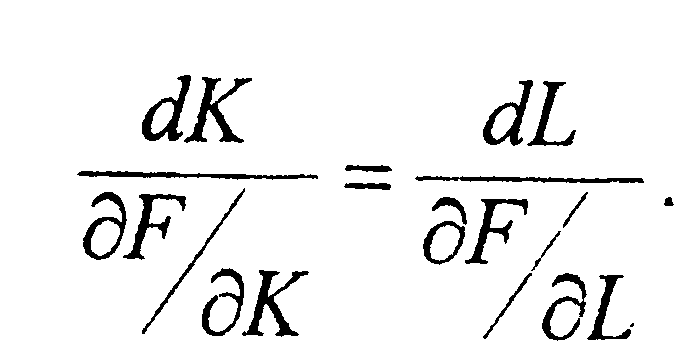
Date: 2015-09-18; view: 673; Нарушение авторских прав