Коэф.эластич.производ.ф-ииот 2х факторов

Важными хар-ми производ.ф-ии явл. коэф. эластич. выпуска по ресурсам.

Е_К = - 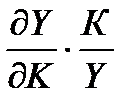Е_L= - 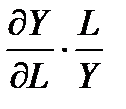Они равняются отношению предельной производительности соответ. рес-са к его сред.производ-ти.

Коэф. эластич. показывает на сколько % изменится выпуск прод-ции при увеличении затрат одного рес-са на 1 % и сохранении зн-я др.рес-са.

Наряду с понятием эластич.выпуска по затратам рес-сов в эк.анализе применяется понятие эластич. взаимозаменяемости рес-сов. При дв-нии вдоль изокванты F(K,L)=Y₀ =const вместе с координатами (.) (K,L) изменяется зн-е , и величина отношения затрат L/K. Считая,что они связаны функциональной завис-тью: L/K= в предположении,что ф-я дифф-мая,вычислим эластчность:

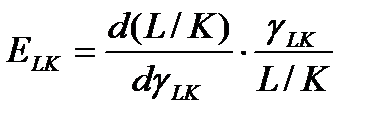. Коэф. эластич. взаимозаменяемости рес-сов Е_LK показыв. на сколько % должно измениться отношение затрат рес-сов,чтобы предельная норма заменяемости рес-сов увелич. на 1%.

Е_LK принимает самые различные зн-я на промежутке [0; 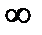). Чем выше зн-е коэф. эластич.взаимозамен.рес-сов,тем в более широких пределах рес-сы могут заменять др.др. При Е_LK=0 возможность замены рес-сов-отсутствует.При Е_LK→ 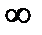рес-сы могут заменять др.в самых широких пределах.Рассмотрим геометрический смысл коэффициента эластичности взаимозаменяемости ресурсов 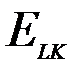. Для этого представим уравнение изокванты 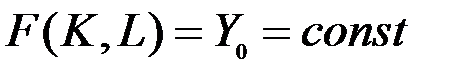в виде 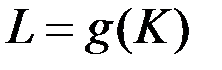, а график последней зависимости изобразим на плоскости 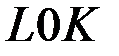рис. 1.1. Соединим точку 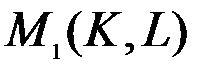с началом координат. Обозначим через 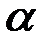угол, который радиус образует с положительным направлением оси 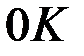, а через 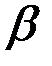- угол наклона касательной, к графику функции 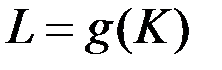, проведенной в точке .

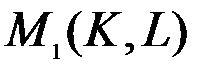Из геометрического смысла производной вытекает, что 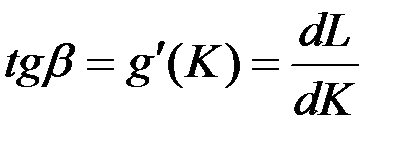, а из треугольника получаем 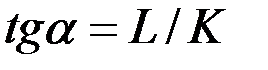. По определению предельной нормы замещения ресурсов .

.

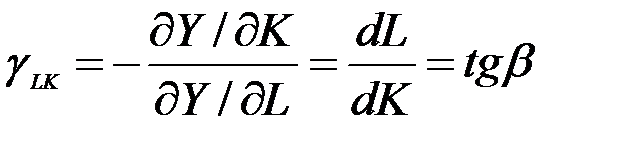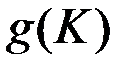
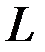
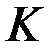
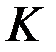
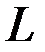
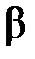
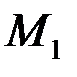
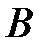
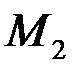
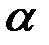
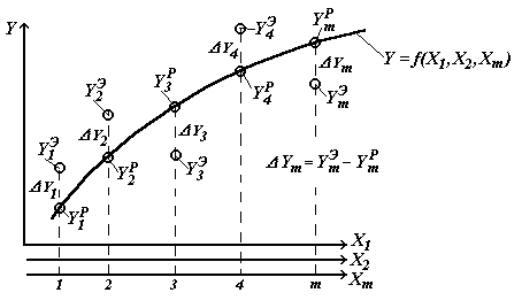
Рис.1.1. График изокванты

При движении точки 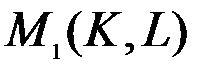вдоль изокванты 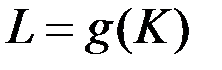вместе с координатами точки изменяется и величина каждого из углов. Тогда коэффициента эластичности взаимозаменяемости ресурсов 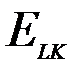показывает на сколько процентов изменится 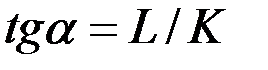, если при переходе по изокванте из точки 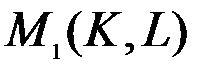в точку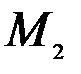 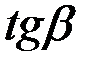увеличиться на один процент.

Коэффициент 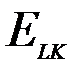удобен для характеристики производственных функций, поскольку для ряда используемых на практике производственных функций он постоянен, т.е. не только не изменяется при движении вдоль данной изокванты, но и не зависит от выбора изокванты. В качестве примера рассмотрим производственную функцию Кобба – Дугласа. Для нее, как отмечалось ранее, 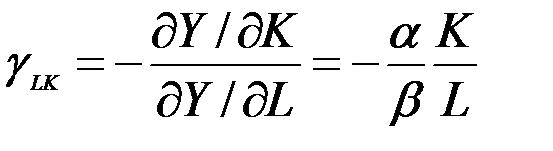. Отсюда 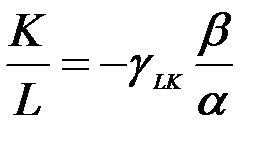, а тогда 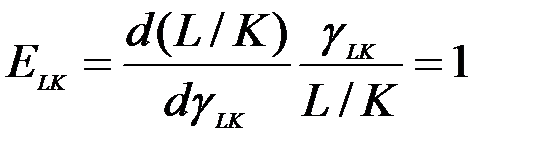. Аналогично вычисляется .

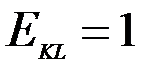Можно показать, что коэффициент эластичности взаимозаменяемости ресурсов принимает самые различные значения на промежутке 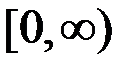. Чем выше значение коэффициента эластичности взаимозаменяемости ресурсов, тем в более широких пределах ресурсы могут заменять друг друга. При 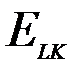= 0 возможность замены ресурсов отсутствует. При стремлении 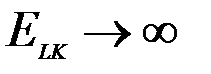ресурсы могут заменять друг друга в самых широких пределах.

Date: 2015-09-18; view: 457; Нарушение авторских прав