Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Функция непрерывных процентов
|
|
Рассмотрим алгоритм формир-я ф-ции непрер. %. Для этого обозначим через Q сумму вклада по истеч-ии n периодов времени, а через Q0 – первонач. 𝛴(депозит), помещ. в банк под 100% годовых.Через год 𝛴 депозита составит Q1 =2Q0, а через полгода-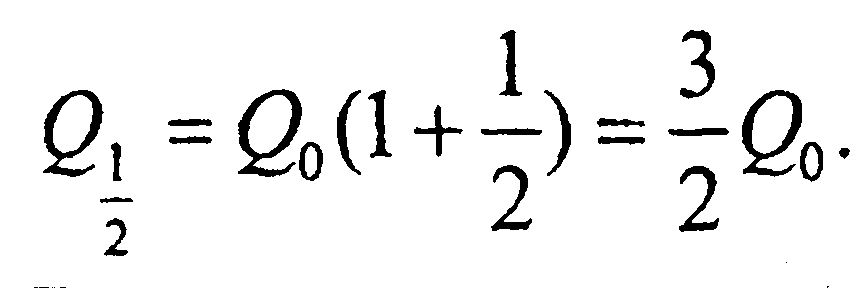 
Пусть последняя 𝛴 вновь будет помещена в кач-ве депозита в том же банке. В этом случае в конце года депозит составит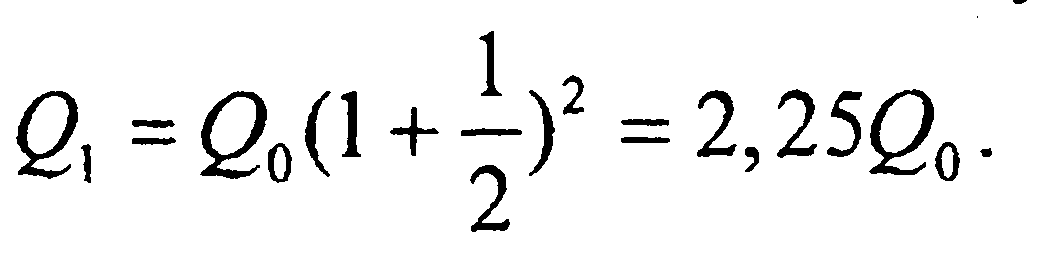 
Если депозит помещать ежеквартально, то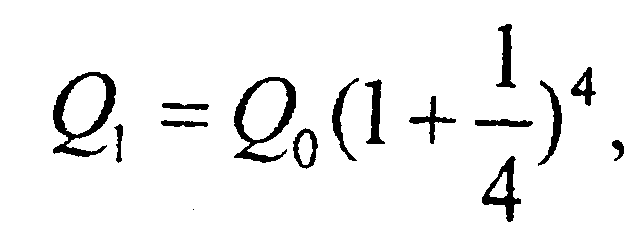 
, а при ежемесячном размещ-ии в конце года депозит составит 
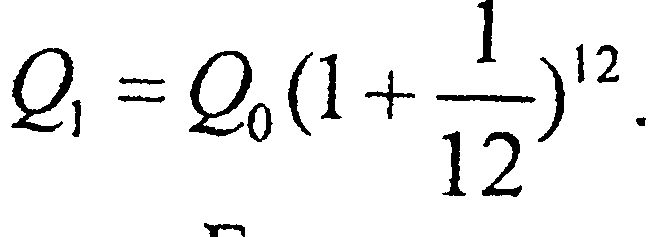Аналогично при ежеднев.: 
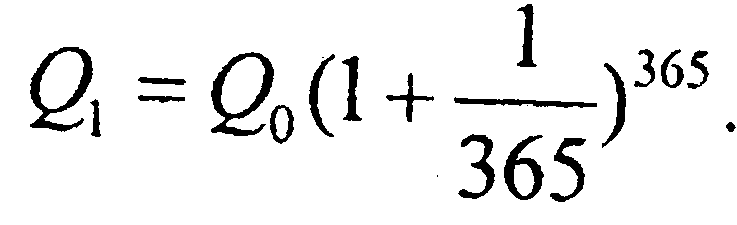Если операцию открытия-закрытия счета производить непрерывно, то к концу года депозит составит 
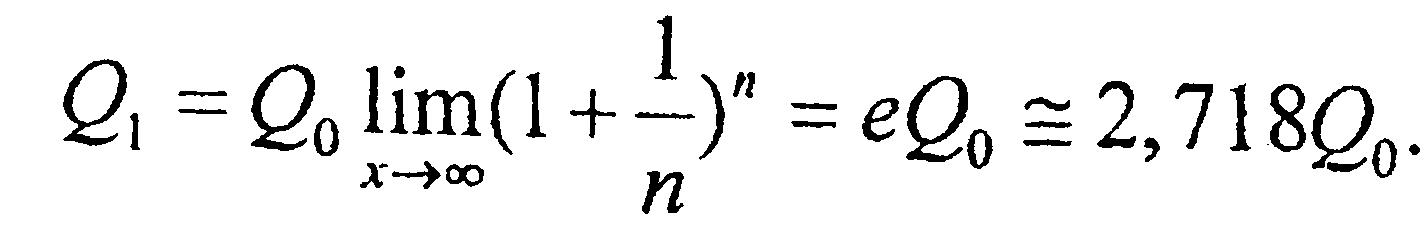Т. о., при номинальной ставке 100 % и непрерывном начислении % доход за год может составить не более 172 %. В общем, но реальном, а не идеализированном случае, если % начисления р, а год разбит на п частей, то через t лет 𝛴 депозита достигнет величины 
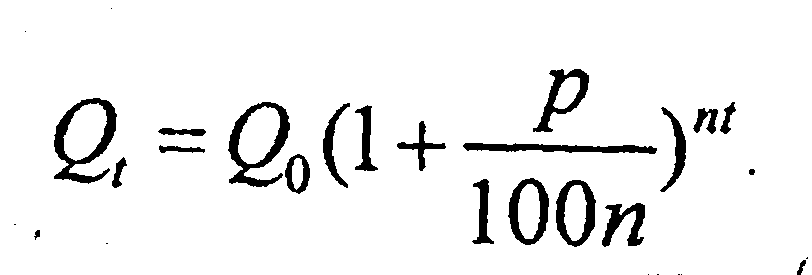Если обозначить через r= p/100, то последнее выр-е можно привести к виду: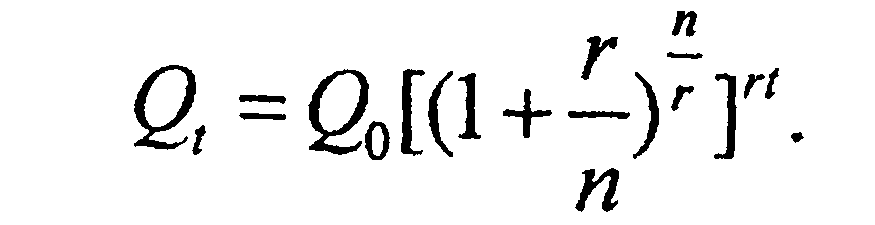 
Если далее устремить п к бесконечности, то сумма Q0, вложенная в банк под р %годовых, за t лет достигнет теоретически предельной суммы
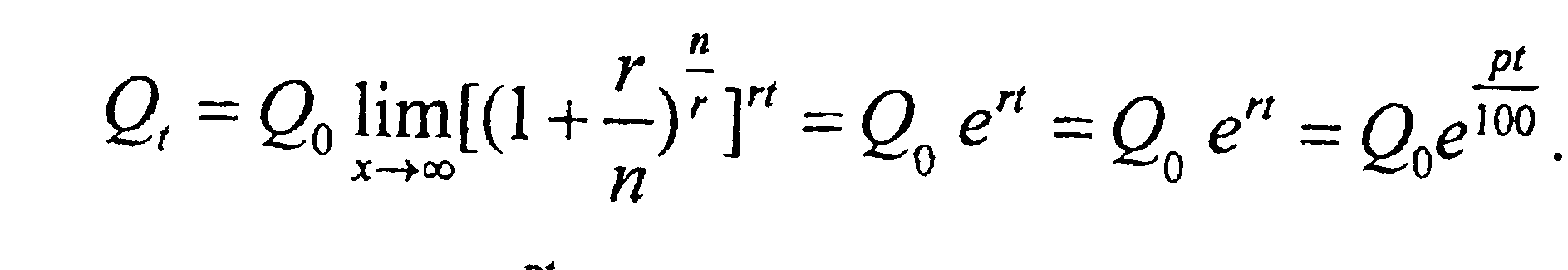Соотн-е 
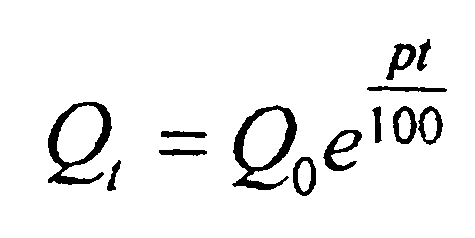предст-ет собой ф-wb. непрерыв. %, где в кач-ве аргумента выступает t= 1,2,…n
13. Логарифмическая производная. Ставка банковского % по кредиту на стр-во.
При выx-ии ставки банковского % исп-ся логарифмическая производная, под которой для положительной функции y=f(x) понимается (1пу)'х.
Дифференцируя функцию Iny как сложную, будем иметь: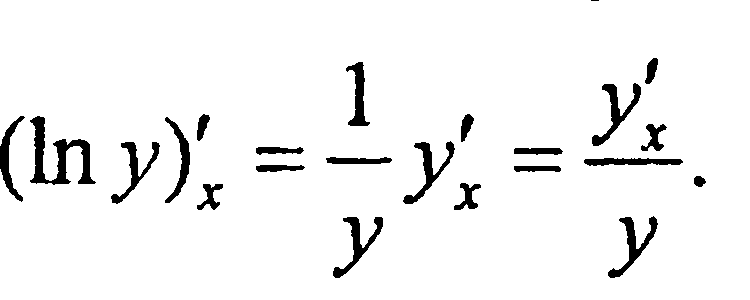 
Поскольку пр-ная хар-ет ск-ть изм-ия ф-ции,то величину y’/y — естественно считать как относит. ск-ть изм-я функции. В эк-ке (Iny)’x называют темпом роста ф-ции y. В общем сл-е, если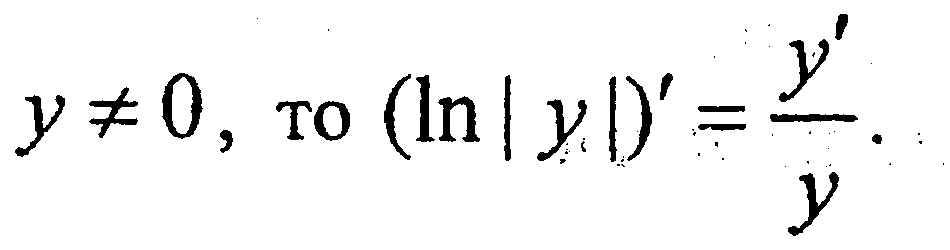 
Рассмотрим ф-цию Qt предст. собой величину вклада (депозита) в момент времени t. Пусть % нач-ся один раз за период времени ∆t. Необходимо определить годовую ставку банковского % r по функции Qt, % за период ∆t сост- ют
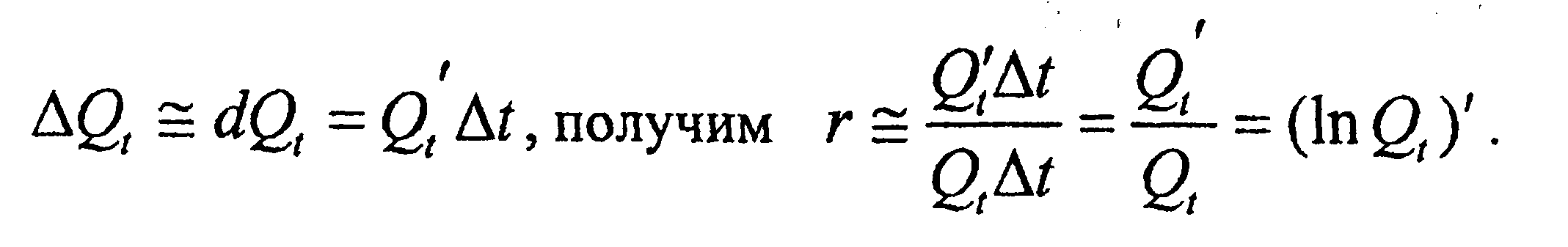
Т.о., ставка банк. % совпадает с логарифмич. производной от вел-ны вклада. Ранее мы установили, что ф-ция непрерыв. % Q имеет вид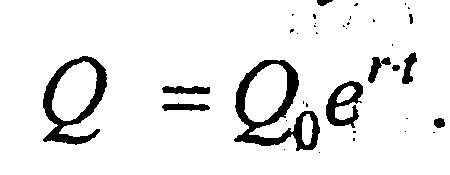 
Рассмотрим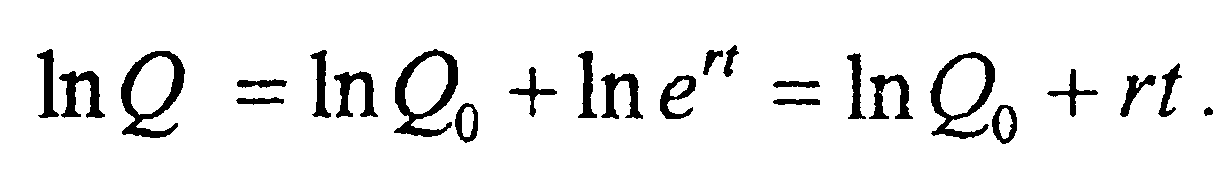 
Тогда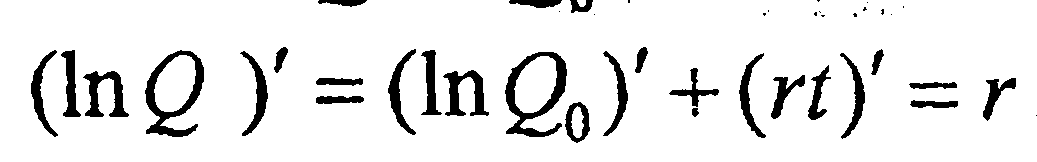 
след., логаримич. пр-ная ф-ции непрер. % = год. ставке банк. %.
14. Производсв. ф-ции в стр. области. 15. Пр-ная ф-ция одной переем. Типы пр-ных ф-ций 2-х переменыых. Пр-ная ф-ция одной перемен. - ф-ция, независ. переем. кот. прин. зн-я объемов затрач. р-са (ф-ра пр-ва), а завис. перем. предст. собой зн-я объемов выпускаемой прод-ции. Ее представляют в традиц. форме записи математической функции y= f(x). При этом для нее характерно, что как у так и х принимают только положит. зн-я. Производств. ф-ция у = f(x) называется одноресурсной или однофакторной. Запись у = f(x) означает, что если ресурс затрачивается в количестве х ед., то прод-ция выпускается в количестве у ед. Символ f означает правило, по кот/ пр-ная система преобразует ресурс в выпуск. В кач-ве примера ф-ция видв y=f(x)= axb. Она обладает св-вом уменьшения приращения ф-ции при увел. аргумента при одном и том же цриращении аргумента. Это позволяет ее исполmp/ в кач-ве производственной ф-ции для тех пр-в, в кот. с ростом величины затрачиваемого ресурса объем выпуска проl-ции растет, однако, при этом каждая доп/ единица р-са дает все меньший прирост объема выпускаемойпрод--ции. Пр-ная ф-ция 2-х переем..
На практике чаще имеют место след. нер-ва противопол. смысла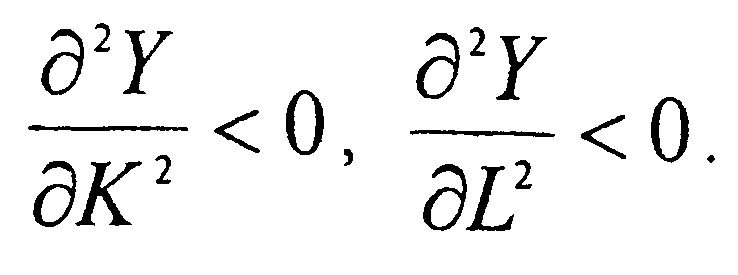 
Опыт показывает, что вусловиях чисто экстенсивного роста пр-ва (увелич. объем пр-ва без изменения технологии) увелич. затрат лишь одного производств. р-са приводит к снижению его эфф-ти. Это связано с тем, что каждая последующая ед. возрастающего р-са соединяется со все меньшим приходящимся на нее кол-вом др. р-са.
Типы пр-ных ф-ций.
Степенная пр-ная ф-ция.. Дост-ва такой ф-ции состоят, во-первых, в наличии небольшого числа параметров, имеющих явный эк. смысл, и, во-вторых, в сущее-нии производных высших порядков. Кроме того, степенные пр-ные ф-ции с помощью логарифмирования сводятся к функциям линейным (относительно новых логарифмических переменных), что удобно для оценки параметров по статистическим данным.
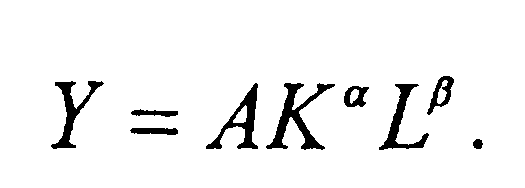
Функция с фиксированными пропорциями ресурсов (функция Леонтьева). Эта функция имеет вид
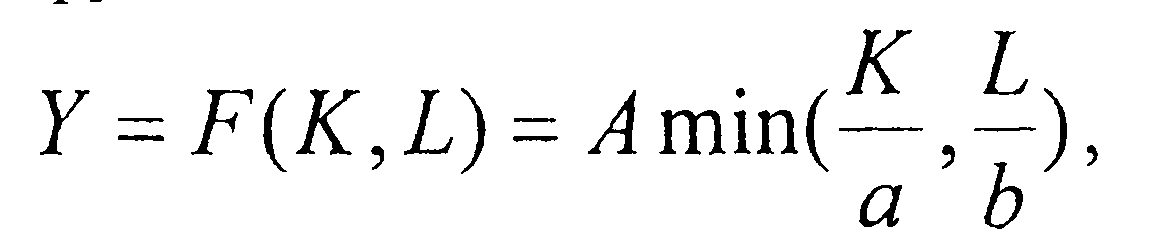
где а,Ь - параметры. Параметры хар-т удельные затраты капитала и труда, необходимые для выпуска прод-ции в кол-ве А. Ф-ция Леонтьева предназначена в основном для моделирования строго детерминированных технологий, которые не допускают отклонения от технологических норм и нормативов использования ресурсов на ед. прод-ции
Date: 2015-09-18; view: 420; Нарушение авторских прав