Погрешность аппроксимации функции

При построении экономико-математических моделей возникают задачи замены табличных 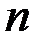опытных значений результирующего показателя (зависимая переменная) 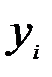и фактора (независимая переменная)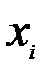 аналитической аппроксимирующей функцией 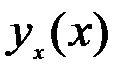. Метод построения аппроксимирующей функции носит название метода наименьших квадратов. Опытные данные – это данные наблюдения над эконом-и процессами (стат. данные) в зависимости м/у 2мя переменными Вычисленные значения аппроксимирующей функции 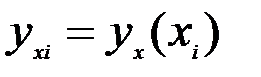при соответствующих значениях фактора 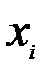обычно отличаются от опытных значений. Эти аналитические значения считают теоретическими, а им соответствующие 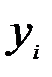- опытными значениями. В дальнейшем опытные значения будем принимать за истинные. Для оценки Степень близости теоретических и опытных значений характеризуют погрешность аппроксимации функции. Различают абсолютную и относительную, локальную и среднюю погрешности.

Модуль разность между теоретическим 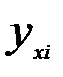и опытным 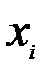значением результирующего показателя, вычисленной при конкретном задании фактора 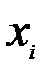, называют абсолютной локальной погрешностью результирующего показателя и обозначают 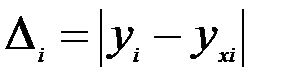. Кроме абсолютной локальной погрешности рассматривают также относительную локальную погрешность как отношение абсолютной погрешности к модулю опытного значения результирующего показателя

.

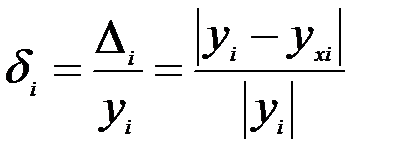Для характеристики погрешности на всем промежутке изменения фактора рассматривают среднюю абсолютную и относительную погрешности. Их вычисляют по следующим соотношениям:

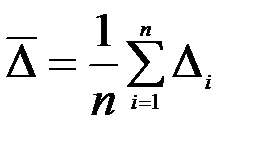и .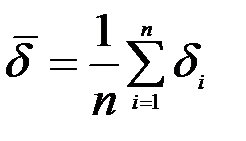

6. Функции спроса и предложения строительных услуг .1)Спрос – это платежеспособная потребность покупателя, т.е. потребность покупателя, располагающего ден. ср-вами для приобретения тов. и усл. На спрос влияют 3 фактора: 1) потребность человека в продукте, 2) цена продукта, 3) уровень ден. доходов потребителя. В основе рыночного спроса на тов. или услугу есть правило(з-н убывающей полезности): Чем выше цена, тем меньше тех, кто согласиться купить данный товар, т.е. уменьшается уровень спроса и наоборот. График имеет вид убывающей кривой, а ее аналит. выр-е: 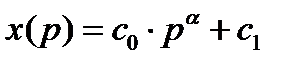, где С₀, С₁принадл. R.

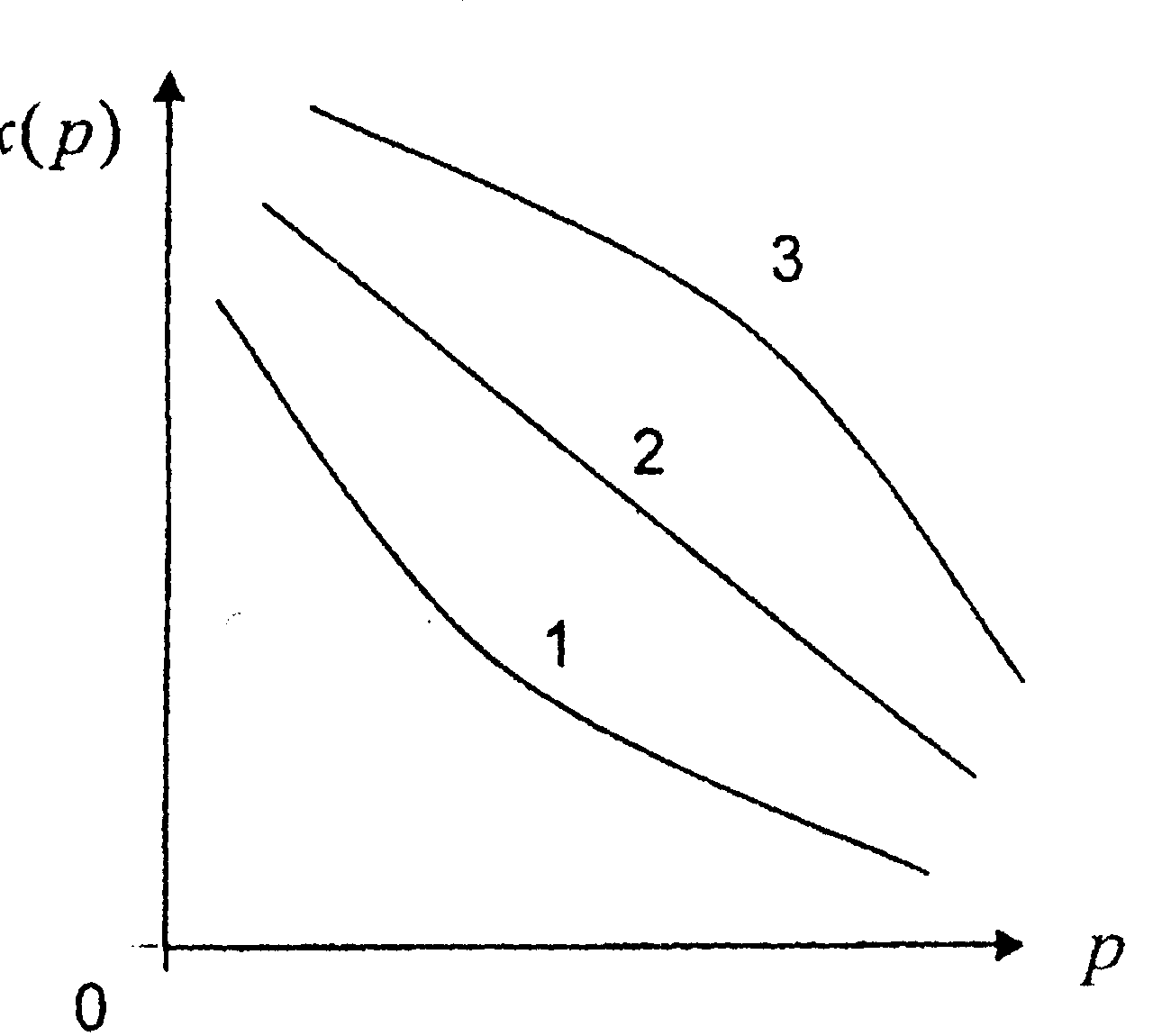
1. Со>0, C1>0,α<0,p>0. 2. Со>0, C1<0,α=1. 3. Со<0, C1>0,α>0 (α≠1). Со и С1 – зависят от числа покупателей на рынке, от ден. доходов и вкусов потребителя, от цен конкурентов и цен на замещающие товары. Общее св-во 1, 2, 3 – отрицательное значение x'(p). 2) Предложение – зеркальное отображение теории спроса. Все продавцы стремятся получить на рынке самую высокую цену, и чем выше цена, тем активнее будет расти предложение товаров. Определяющий фактор, влияющий на предложение тов. – издержки пр-ват.е. сумма ден. расходов на пр-во прод-ции.Чем меньше издержки, тем меньше цена. Предложение – совокупность товаров, представленных к продаже по соотв-м, удовл-м товаропроизводителя ценам. Кривая предложения –это кривая предельных издержек фирмы на пр-во кажд. новой единицы продукции. Как видно из графика сниж-е цены p(x) ведет к соотв. измен-ю предлож-я товаров ч, повыш-е цен ведет к росту предл-я. 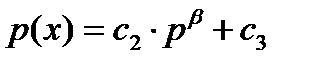.С2 и С3 зависят от цены товара, числа продавцов на рынке, налогов, технологии пр-ва, цен на ресурсы.

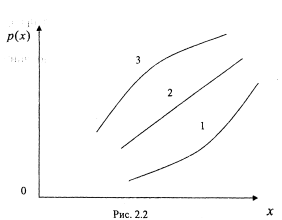
1. С2>0,C3>0,β>1, x>0,p>0. 2. С2>0,C3>0,β=1. 3. С2>0,C3>0,0<β<1. Общее св-во 1, 2, 3 – положительное значение p'(x).

7. Функция спроса по цене. 1)Спрос – это платежеспособная потребность покупателя, т.е. потребность покупателя, располагающего ден. ср-вами для приобретения тов. и усл. На спрос влияют 3 фактора: 1) потребность человека в продукте, 2) цена продукта, 3) уровень ден. доходов потребителя. В основе рыночного спроса на тов. или услугу есть правило(з-н убывающей полезности): Чем выше цена, тем меньше тех, кто согласиться купить данный товар, т.е. уменьшается уровень спроса и наоборот. График имеет вид убывающей кривой, а ее аналит. выр-е: 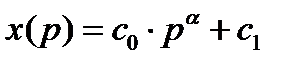, где С₀, С₁принадл. R.

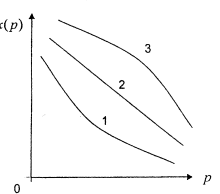
1. Со>0, C1>0,α<0,p>0. 2. Со>0, C1<0,α=1. 3. Со<0, C1>0,α>0 (α≠1). Со и С1 – зависят от числа покупателей на рынке, от ден. доходов и вкусов потребителя, от цен конкурентов и цен на замещающие товары. Общее св-во 1, 2, 3 – отрицательное значение x'(p).

Функции спроса (предложения) по цене могут быть как линейными, так и нелинейными. В случае линейной функции она имеет следующий вид: 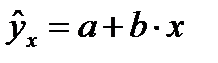Функция характеризует собой семейства прямых, каждая из которых характеризуется конкретными значениями коэффициентов a и b. Наилучшей для рассматриваемой выборки из всего множества прямых является, та прямая, которая на плоскости xoy расположена «ближе» всего, в определенном смысле, к опытным точкам. В качестве меры близости прямой и некоторой точки на плоскости можно выбрать расстояние между ними. При этом под расстоянием следует понимать модуль разности между опытным (наблюдаемым) значением результирующей величины и теоретическим, вычисленным по формуле при одном и том же значении фактора т.е. 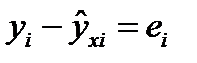(i=1,2,...,n)

В качестве критерия близости между прямой и множеством точек на плоскости целесообразно выбрать минимум суммы квадратов этих расстояний. 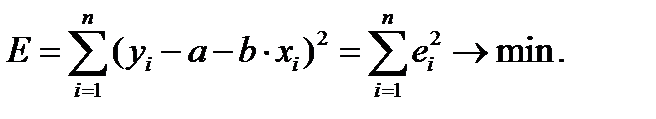Здесь считается, что 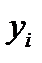и 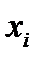- известные статистические данные; a и b – неизвестные параметры (коэффициенты) линии регрессии. Поскольку функция 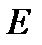непрерывна, выпукла и ограничена снизу нулем, то она имеет минимум.

Изложенная идея минимизации суммы квадратов отклонений (на плоскости расстояний) опытных от теоретических значений объясняемой переменной положена в основу метода наименьших квадратов.

«Наилучшая» по методу наименьших квадратов прямая линия всегда существует. Вместе с тем, это не означает, что она является наилучшей среди всех возможных функций, например, в сравнении с нелинейными.

Date: 2015-09-18; view: 3152; Нарушение авторских прав