Приклад. Поле комплексних чисел Cє простим розширенням поля дійсних чисел R, яке одержане приєднанням одного елемента – уявної одиниці

Поле комплексних чисел Cє простим розширенням поля дійсних чисел R, яке одержане приєднанням одного елемента – уявної одиниці.

u Нехай F – поле. Якщо множина L є абелевою гупою з операцією додавання, визначена операція множення елементів 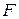(скалярів) на елементи 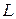(вектори), що не виводить за межі 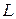, і для будь-яких x, h 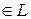, 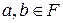виконуються умови:

1) ;

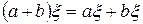2) ;

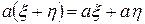3) ;

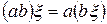4) ,

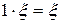то L називається лінійним векторним простором над F.

ТЕОРЕМА 18. Будь-яке розширення поля F є лінійним векторним простором над F.

4Розширення, як і будь-яке поле, є абелевою групою за додаванням. Неважко також бачити, що умови 1) – 4) виконуються.3

u Система елементів розширення 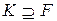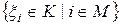( 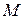– скінченна або нескінченна множина натуральних індексів), для якої виконується умова 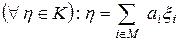, , називається базисом 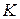над F.

u Якщо в розширенні 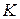поля F існує базис із скінченною кількістю елементів, то 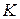називається скінченним розширенням F.

u Розмірність 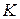як лінійного векторного простору над полем F називається степенем розширення 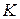і позначається .

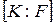Date: 2015-09-18; view: 350; Нарушение авторских прав