Задачі до §3

1. Довести:

а) степінь суми поліномів не перевищує максимальної з степенів поліномів, що додаються;

б) степінь добутку поліномів не перевищує суми степенів співмножників;

в) в цілісному кільці степінь добутку поліномів дорівнює сумі степенів співмножників.

2. Довести:

а) R комутативне Û R[X] комутативне;

б) R кільце з одиницею Û R[X] кільце з одиницею;

в) R цілісне кільце Û R[X] цілісне кільце.

3. Що таке оборотні елементи кільця F[X], де F – поле?

4. Знайти (f, g) над F₃ і представити його у вигляді лінійної комбінації вказаних поліномів: .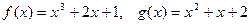

5. Для поліномів f ₁,…, f_п довести:

а) deg(НОД(f ₁,…, f_п)) £ deg(НОД(f ₁,…, f_m)) при m £ n;

б) (f ₁, f ₂, f ₃)=(f ₁, (f ₂, f ₃).

6. Нехай R – евклідове кільце, що не містить оборотних елементів, крім±1. Чи можна стверджувати, що R[X] – також евклідове кільце?

7. Використовуючи тотожності

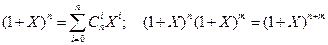, довести: .

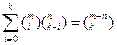8. Довести критерій незвідності поліномів 2го та 3го степеню:

Нехай F– поле, 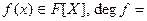2 або 3. Тоді f (x) незвідний тоді і тільки тоді коли f (x) не має коренів в F.

Date: 2015-09-18; view: 318; Нарушение авторских прав