Краевые условия задачи Молоденского

В точке на физической поверхности Земли нам известно значение потенциала тяжести 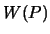, а в точке 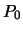на теллуроиде -- значение нормального потенциала 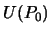. Используя векторно-матричную математику запишем основные соотношения, связывающие возмущающий потенциал разность потенциалов 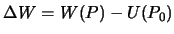, так называемую аномалию потенциала, аномалию высоты 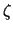и смешанную аномалию силы тяжести .

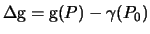Нетрудно видеть, что на теллуроиде Молоденского , на теллуроиде Марусси 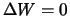, а на теллуроиде Крарупа . В общем случае имеем

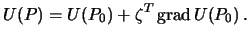
(9.6)

Тогда 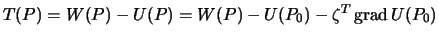или

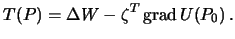
(9.7)

Аналогично получим смешанную аномалию

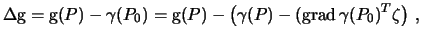
(9.8)

но градиент вектора g есть градиент всех его составляющих, что дает матрицу-тензор. Обозначим

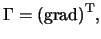
поэтому

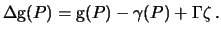
Заметим, что разность 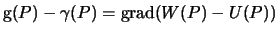, есть так называемая "чистая" аномалия, равна градиенту возмущающего потенциала 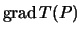, поэтому вместо (9.8) можно записать

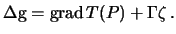
(9.9)

Итак, мы получили два уравнения, которые на физической поверхности Земли 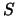можно взять в качестве краевых условий

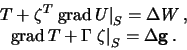
(9.10)

Первая из приведенных формул есть обобщение формулы Брунса, связывающей возмущающий потенциал с высотой квазигеоида. Из этих двух уравнений можно построить одно, если исключить аномалию высоты 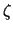. Решим второе из приведенных уравнений. Предполагая, что матрица 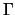неособая, получим 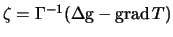. Подставим найденное решение в первое уравнение. Заметим, что

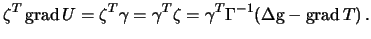
(9.11)

Подставляя полученное выражение в первое уравнение из (9.10), будем иметь

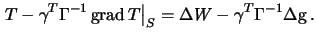
Для упрощения записи, введем обозначение 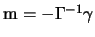. Теперь краевое условие обобщенной задачи Молоденского принимает вид

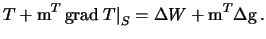
(9.12)

9.3.1 Частный случай: измерения выполнены на уровенной поверхности

Рассмотрим случай, когда аномалия потенциала -- постоянная величина. Другими словами точка , как и в задаче Стокса, находится на поверхности уровня. Тогда . Выберем локальную систему отсчета с началом в точке 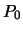. Ось направим на север, ось -- на восток, а ось 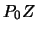-- по направлению внутренней нормали к эллипсоиду вниз. Тогда вектор аномалии высоты может быть определен матрицей-строкой

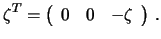
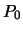Градиенты нормального потенциала в точках и равны

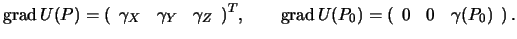
Матрица вторых производных нормального потенциала

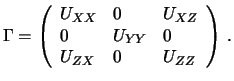
Первое из уравнений (9.10) для краевых условий дает

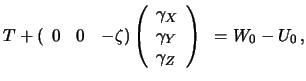
то есть

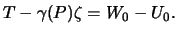
Следовательно,

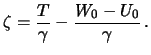
(9.13)

Второе уравнение из (9.10) выглядит следующим образом

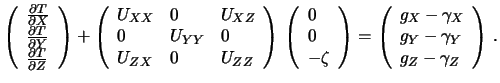
(9.14)

Первые два уравнения дают уклонения отвеса

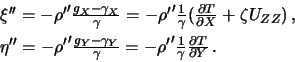
(9.15)

где 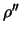=206265 -- число секунд в радиане. Последний член в скобках формул (9.15) дает очень малый вклад и может быть отброшен. Действительно, мы видели, что для нормальной силы тяжести максимальное значение горизонтального градиента равно 0,000811 мГал/м. При 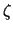=100 м, что бывает очень редко, величина 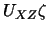составит 0,081 мГал и внесет погрешность в уклонение отвеса 0,017", тогда как уклонения отвеса достигают несколько секунд дуги.

Третье уравнение имеет вид 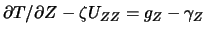. Подставив сюда величину 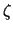из (9.13) получим краевое условие для смешанных аномалий

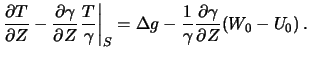
(9.16)

Мы получили, таким образом, краевое условие почти совпадающее с краевым условием Стокса.

Задача определения фигуры Земли сводится к построению решения уравнения Лапласа, которое удовлетворяет краевому условию (9.16) или, в общем случае, условию (9.12). Способы решения этой задачи заслуживают специального изучения, но выходят за пределы нашего курса.

<< Лекция 8. Определение фигуры геоида | Оглавление |

Date: 2015-09-05; view: 553; Нарушение авторских прав