Система высот

Определить фигуру какой-либо поверхности -- это значит определить расстояния каждой точки этой поверхности до тела отсчета, за которое берется эллипсоид вращения. Эти расстояния обычно называют геодезическими высотами. Понятие высоты, на первый взгляд, не требует уточнения. Однако это не так. М.С.Молоденский разработал целую систему высот для геодезии.

Допустим, что имеем две точк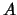и и 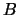, причем точка 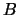выше точки 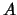. Если соединить эти точки каналом и пустить воду, куда она потечет? Кажется вполне естественным ответ: из точки 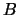к точке 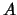. Однако это не совсем так. Весь вопрос в том, как проходит уровенная поверхность через эти точки. Если обе точки лежат на одной уровенной поверхности, то вода никуда не потечет. Если уровенная поверхность, проходящая через точку 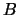окажется под уровенной поверхностью точки 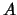, то будет наблюдаться обратная картина: вода потечет от точки 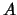к точке 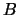. Таким образом, для гидротехнических сооружений система геодезических высот оказывается непригодной.

В геодезии высоты определяют нивелированием. Нивелир -- это оптическая труба, визирная линия которой устанавливается строго горизонтально с помощью достаточно высоко чувствительного уровня. Чтобы определить превышение одной точки над другой, в этих точках устанавливаются специальные вертикальные рейки. С помощью нивелира с каждой рейки поочередно берут отсчеты, тогда разность этих отсчетов есть нивелирное превышение одной точки над другой.

Нивелирный ход от точки 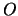, расположенной, например, на уровне моря, к точке даст измеренную высоту точки над уровнем моря 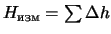, где 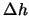нивелирное превышение одного звена. Если нивелирный ход имеет много звеньев, то сумму можно заменить интегралом .

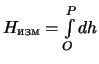Вычислим разность потенциалов меду точкам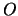и и .

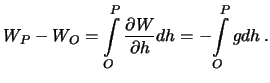
(9.1)

Таким образом, для определения разности потенциалов нужно иметь нивелирные превышения и силу тяжести вдоль всего профиля.

Введем в рассмотрение еще одну точку. Через точку проходит силовая линия, которую можно продолжить до поверхности геоида (уровень моря). Она пересечется с этой поверхностью в токе textitР'. Таким образом точки 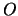и Р' лежат на одной поверхности уровня (на геоиде) Поскольку результат определения разности потенциалов не зависит от пути интегрирования, выберем такой маршрут О-Р'-Р. Приращение потенциала мы получим лишь на отрезке силовой линии Р'-Р: 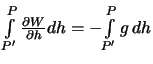. При движении по силовой линии сила тяжести непрерывно меняется. Согласно теореме о среднем, в курсе математического анализа, можно найти такое значение подынтегральной функции, которое она принимает внутри интервала интегрирования, которым можно заменить подынтегральное выражение

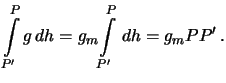
Отрезок силовой линии РР' называется ортометрической высотой точки над уровнем моря (то есть над геоидом). Итак

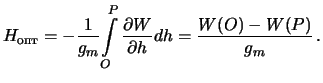
(9.2)

Чтобы вычислить ортометрическую высоту, необходимо знать не только приращение потенциала, но и уметь вычислить среднее значение силы тяжести на отрезке силовой линии, а для этого необходимо знать как меняется сила тяжести на этом отрезке внутри Земли. М.С.Молоденский предложил заменить 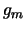на среднее значение нормально силы тяжести. Высоту, которую мы таким образом получим он назвал нормальной. Такая замена неизбежно внесет погрешность, которая, впрочем, невелика. Согласно определению, нормальная высота может быть определена по формуле

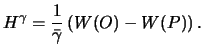
(9.3)

Поскольку ортометрическая высота есть высота точки над уровнем моря, то мало отличающаяся от нее нормальная высота будет равна высоте точки от поверхности мало отличающейся от геоида. Молоденский назвал эту поверхность квазигеоидом.

Отличие истинной (геодезической) высоты от нормальной уместно назвать аномалией высоты. Это понятие также ввел Молоденский. Итак, аномалия высоты есть

(9.4)

Аномалия высоты есть расстояние квазигеоида от эллипсоида, или равна высоте почтигеоида. Очевидно, что 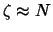. В классическом понимании, определить фигуру Земли -- это значит определить высоты геоида 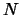. Однако, мы не сделаем большой погрешности, если будем считать фигурой Земли -- фигуру квазигеоида, а для этого мы должны определить аномалии высот.

Сведем задачу снова к краевой задаче для гармонических функций. Следовательно, аномалию высоты нужно определить через возмущающий потенциал (см лекцию 8, раздел 8.1). Итак, имеем:

• потенциал тяжести в точке равен 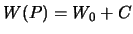, С -- приращение потенциала от уровня моря (точка );
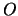• нормальный потенциал в точке 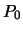, равный .

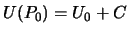Таким образом, точка 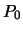не совпадает с точкой , так как она подбирается так, чтобы приращение потенциала реального и нормального были одинаковыми

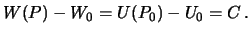
Здесь постоянные 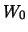и 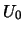означают следующее: первая постоянная есть величина потенциала тяжести на геоиде, а вторая -- величина нормального потенциала на уровенном эллипсоиде. Нетрудно убедиться, что отрезок 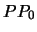равен аномалие высоты 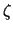. Следовательно

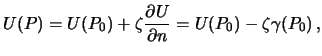
поэтому .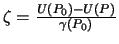

С другой стороны 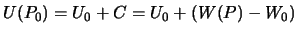, поэтому

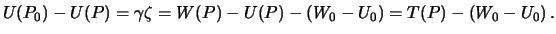
Отсюда следует

(9.5)

Мы получили вновь формулу Брунса, однако она отличается тем, что содержит дополнительный член 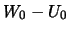, который в "классической" формуле отсутствует. В теории Стокса предполагается, что обе эти постоянные равны: потенциал тяжести на уровне моря равен потенциалу уровенного эллипсоида.

Другое отличие: нормальная сила тяжести задается не на геоиде, а в некоторой точке отстоящей от текущей токи на физической поверхности на величину, равную аномалии высоты. Геометрическое место всех точек 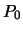называется теллуроидом. Гравитационные аномалии, как и прежде, относятся к разным точкам: наблюденное значение задано на физической поверхности, а нормальное -- на теллуроиде.

В литературе, посвященной исследованию гравитационных полей планет, встречаются и другие определения понятия теллуроида, как поверхности аппроксимирующую форму Земли.

Теллуроид Марусси определяется следующим образом. Теллуроид -- геометрическое место точек, в которых потенциал тяжести совпадает с нормальным .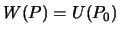

Теллуроид Крарупа (гравиметрический теллуроид) -- геометрическое место точек, в котором нормальная сила тяжести совпадает с силой тяжести на поверхности Земли .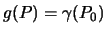

Каждое из определений теллуроида требует своего подхода для определения его фигуры. Мы остановимся здесь лишь на теллуроиде и квазигеоиде Молоденского.

Date: 2015-09-05; view: 755; Нарушение авторских прав