Лекция 8. Определение фигуры геоида

Возмущающий потенциал, гравитационные аномалии. Краевое условие для возмущающего потенциала. Внешние и внутренние краевые задачи Дирихле, Неймана, смешанные краевые задачи. Определение высот геоида методом Стокcа. Функция Стокса. Определение уклонений отвеса. Формулы Венинг-Мейнеса.

8.1 Возмущающий потенциал

Среди специалистов по высей геодезии широко применяется термин возмущающий потенциал, как разность между реальным и нормальным потенциалами в одной точке. Нельзя сказать, что термин удачен. В небесной механике часто употребляется термин возмущающие силы, возмущающая силовая функция, возмущения. Возникает вопрос, что именно возмущает данная сила? Для небесной механики ответ ясен -- закон движения тела, делает его отличным от кеплеровского, невозмущенного. Правда, терминология московской и петербургской школ небесных механиков различаются. Москвичи говорят функция возмущающая, а петербуржцы -- пертурбационная. Так что же "возмущает" возмущающий потенциал? Ответ -- ничего. По-видимому прав австрийский геодезист Г.Мориц, который предлагает ввести термин аномалия потенциала. Говорим же мы аномалия силы тяжести, имея в виду разность реальной и нормальной силы тяжести! Но отдавая дань традиции, мы будем употреблять термин возмущающий потенциал именно как разность реального и нормального потенциалов тяжести или притяжения взятых в одной и той же точке.

Возьмем точку на поверхности геоида -- уровенной поверхности -- с координатами 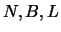, где 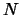геодезическая высота точки (расстояние от уровенной поверхности до эллипсоида) Другими словами это высота геоида в точке . Две другие координаты -- 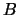и 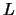соответственно геодезические широта и долгота (см. лекцию 2, раздел 2.3). На поверхности эллипсоида точку с такими же значениями широты и долготы будем обозначать буквой 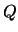. Понятно, что высота этой точки равна нулю. Сила тяжести в точке :

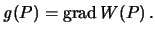
Нормальная сила тяжести в точке :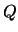

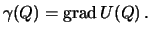
Разность абсолютных значений этих векторов определяет смешанную гравитационную аномалию.

Возмущающий потенциал в точке 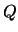(на эллипсоиде) равен

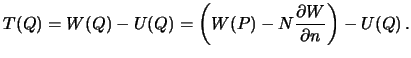
Однако, поскольку , получим

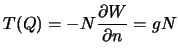
(8.1)

Определим смешанную аномалию

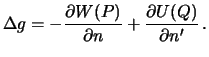
(8.2)

В первом слагаемом мы дифференцируем потенциал по внешней нормали к геоиду, а во втором -- к эллипсоиду. Эти два направления, вообще говоря, не совпадают. Правда, отличие не велико и ошибка составляет всего 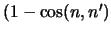, то есть величину порядка квадрата отклонения отвесной линии. Это существенно меньше квадрата сжатия, поэтому в нашем приближении можно не делать различия в направлениях отвесной линии и нормали к эллипсоиду.

"Опустим" значение силы тяжести из точки в точку 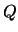, применяя формулы линейного приближения

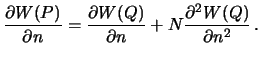
(8.3)

Вертикальный градиент силы тяжести, как мы видели (см. лекцию 7, уравнение (7.12)), зависит от радиусов кривизны нормальных сечений и угловой скорости вращения Земли

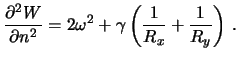
(8.4)

Пренебрегая малыми порядка 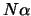, можно пренебречь и членом 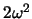. Кроме того, поскольку 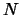также малая величина (сравнению с 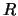), можно не учитывать различия между радиусами кривизны меридионального сечения и сечения в первом вертикале. После упрощений, формула (8.3) принимает вид

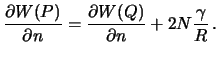
(8.5)

Теперь смешанную аномалию можно записать так

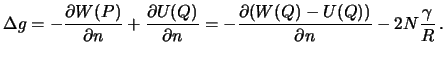
Разность 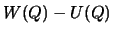есть возмущающий потенциал в точке 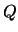, а тот, в свою очередь, связан с высотой геоида 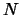формулой (8.1). Заменяя в этой формуле реальное значение силы тяжести на нормальное, получим 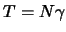. Теперь смешанную аномалию можно выразить через возмущающий потенциал следующим образом

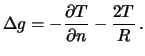
(8.6)

Итак, задача определения фигуры геоида (поверхности уровня относительно эллипсоида) сводится к определению гармонической функции Т -- возмущающего потенциала, который линейно связан с высотой геоида. Проблема интегрирования уравнения Лапласа, при условии, что на заданной поверхности искомая функция подчиняется некоторому условию, которое называют краевым условием, принадлежит к большому классу краевых задач, с некоторыми из них мы и познакомимся.

Date: 2015-09-05; view: 606; Нарушение авторских прав