Краевая задача Дирихле для сферы

Попытаемся решить следующую задачу. Дано дифференциальное уравнение Лапласа, определяющее функцию 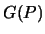, гармоническую в некоторой области, ограниченной замкнутой поверхностью 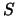. Все значения этой функции на границе области, то есть на поверхности 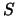, известны. Из всех решений уравнения Лапласа требуется выбрать только те, которые удовлетворяют краевому условию. Решение этой задачи существенным образом зависит от вида граничной поверхности. Покажем, как она решается, если заданная поверхность -- сфера. В данной формулировке имеем дело с внутренней проблемой Дирихле.

Иногда требуется определить гармоническую функцию вне граничной поверхности. Тогда это внешняя проблема Дирихле.

Допустим, что искомая функция 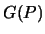задана на поверхности сферы 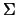значениями 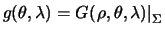. Разложим функцию 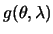в ряд Лапласа:

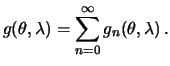
Внутренняя проблема Дирихле	Внешняя проблема Дирихле
Искомым решением будет	Решение уравнения Лапласа задают в виде суммы шаровых функций второго рода
(8.7)	(8.8)
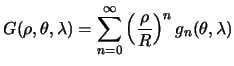
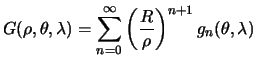
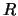так как: удовлетворяет уравнению Лапласа, как шаровая функция первого рода; на сферической поверхности радиуса она равна .	Эта функция также: удовлетворяет уравнению Лапласа как шаровая функция второго рода; на поверхности она равна 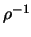; на бесконечности стремится к нулю как , что говорит о ее регулярности на бесконечности.