Определение высот геоида

Мы убедились в том, что возмущающий потенциал является гармонической функцией и на сфере выполняется краевой условие (8.6). Это типичная внешняя смешанная краевая задача. Чтобы ее решить, нужно представить смешанную гравитационную аномалию рядом Лапласа

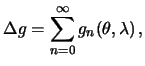
где

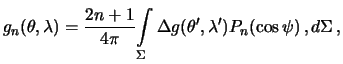
(8.14)

где 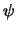-- сферическое расстояние между точкой 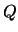и элементом сферической поверхности 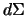. Представим теперь правую часть уравнения (8.6), задающее краевое условие. Для возмущающего потенциала справедливо разложени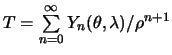е , где

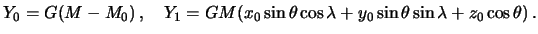
В классическом решении данной задачи, получившей название задачи Стокса, предполагается, что масса эллипсоида равна массе реальной Земли, то есть 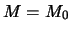, а начало координат совпадает с центром масс планеты 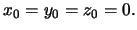Отсюда следует, что разложение возмущающего потенциала начинается с :

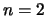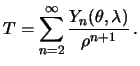
Пренебрегая квадратом сжатия, мы снова дифференцирование по нормали заменим дифференцированием по радиус-вектору

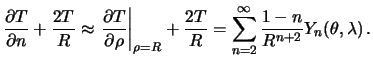
Следовательно

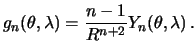
Заметим, что при 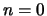, должно быть

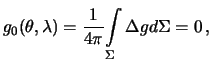
а при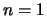

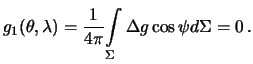
Итак, для того, чтобы решение задачи Стокса существовало необходимо, чтобы среднее значение смешанных гравитационных аномалий равнялось нулю и, кроме того, должен равняться нулю интеграл 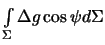. Теперь решение краевой задачи для возмущающего потенциала принимает вид

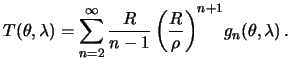
(8.15)

Подставим сюда интегральную форму (8.14) для функций Лапласа:

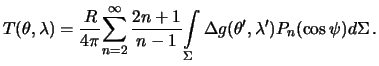
(8.16)

Поскольку интегрирование ведется по сфере радиуса 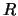в формуле (8.16) мы полагали 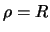. Введем обозначение

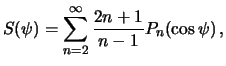
(8.17)

и решение задачи Стокса принимает окончательный вид

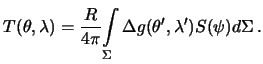
(8.18)

Функцию 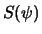часто называют функцией Стокса. В (8.17) она задана в виде разложения по степеням полиномов Лежандра от косинуса центрального расстояния 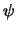. Ее "компактный" вид следующий

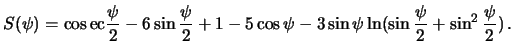
Легко видеть, что точка 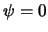-- особая. Здесь функция Стокса обращается в бесконечность, тем не менее интеграл (8.18) сходится, но при выполнении двух указанных выше условий, которым должны удовлетворять гравитационные аномалии. Используя формулу (8.1), которую часто называют формулой Брунса, из возмущающего потенциала легко получить высоты геоида

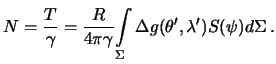
(8.19)

Date: 2015-09-05; view: 463; Нарушение авторских прав