
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Посточнные Стокса
|
|
Постоянной Стокса называется величина, которая определяется следующим образом
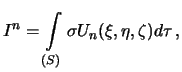
| (5.5) |
где 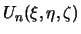 гармоническая функция внутри объема интегрирования.
гармоническая функция внутри объема интегрирования.
Вернемся к формуле (5.3). Воспользуемся формулой сложения гармонических функций (4.19). Ее, очевидно, можно переписать следующим образом
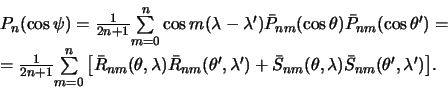
Следовательно
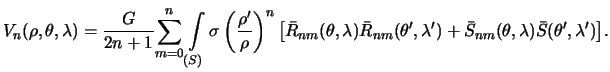
| (5.6) |
Функции текущих (штрихованных) координат 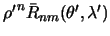 и
и 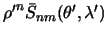 являются гармоническими, так как они принадлежат к шаровым функциям первого типа. Следовательно, по определению (5.5) интегралы вида
являются гармоническими, так как они принадлежат к шаровым функциям первого типа. Следовательно, по определению (5.5) интегралы вида 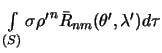 и
и 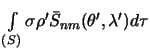 являются стоксовыми постоянными.
являются стоксовыми постоянными.
Введем обозначения
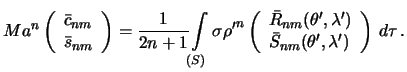
| (5.7) |
Здесь, как несколько позже убедимся, М -- масса тела, а -- постоянная, имеющая размерность длины, а 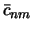 и
и 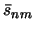 безразмерные постоянные Стокса.
безразмерные постоянные Стокса.
Теперь функцию Лапласа для потенциала притяжения во внешней точке
Можно представить следующим образом
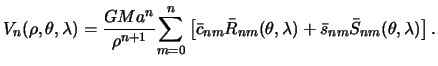
| (5.8) |
Суммируя по всем 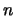 , получим искомое разложение потенциала притяжения в ряд Лапласа
, получим искомое разложение потенциала притяжения в ряд Лапласа
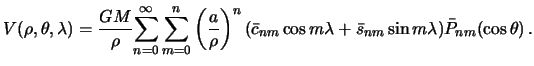
| (5.9) |
Все рассуждения мы провели для нормированных функций, отмечая их чертой сверху. Однако эти же рассуждения справедливы и для ненормированных функций. В этом случае постоянные Стокса будут иметь несколько иной вид. Опуская выкладки, приведем лишь окончательную формулу
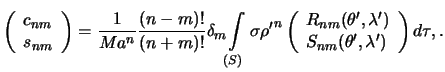
| (5.10) |
где  при
при 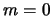 и
и 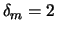 при
при 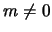 .
.
Date: 2015-09-05; view: 582; Нарушение авторских прав