Разложение гравитационного потенциала в ряд Лапласа

Напомним, что под потенциалом какой либо силы, в том числе и силы тяжести мы будем понимать силовую функцию. Для начала остановимся на потенциале сил притяжения, который чаще всего называют гравитационным потенциалом. Пусть элемент массы dm находится в точке Q 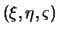, а точка P(x,y,z) с фиксированными координатами находится вне притягивающего тела. Радиус-вектор, соединяющий точки Р и Q, будем обозначать через 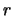, а радиус-векторы этих точек соответственно через 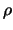и 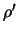. Угол между этими векторами будем обозначать через 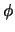. Если точка О -- начало координат, то из треугольника ОРQ следует

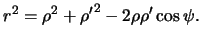
Потенциал притяжения тела в точке имеет вид

(5.1)

где 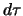-- элемент объема, 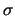-- плотность. Вынесем из-под знака корня величину 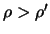, получим

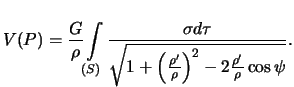
Под знаком интеграла стоит производящая функция полиномов Лежандра (см. формулу (4.1)), поэтому

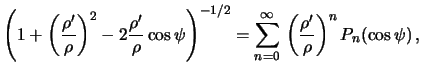
где 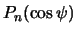-- полином Лежандра степени .

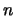Теперь потенциал притяжения в точке принимает вид

(5.2)

Каждое отдельное слагаемое полученной формулы есть функция Лапласа для потенциала притяжения во внешней точке. Обозначив ее через 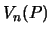, получим

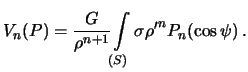
(5.3)

Теперь ряд Лапласа можно записать так

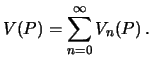
(5.4)

Функции Лапласа, как следует из формулы (5.3), зависят от распределения плотности внутри притягивающего тела. Приведенный интеграл есть постоянная величина, которая, в свою очередь, определяется с помощью так называемых постоянных Стокса, или, стоксовых постоянных.

Date: 2015-09-05; view: 538; Нарушение авторских прав