
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Аналитическое представление функции, заданной на поверхности сферы, рядом Лапласа
|
|
Свойство ортогональности сферических функций делает их незаменимыми для аналитического представления физического поля, рельефа или других величин, заданных в виде карты на сферической поверхности. Сферические функции играют ту же роль, что и тригонометрические для приближенного представления произвольной функции, заданной на отрезке рядом Фурье. Ряд, заданный в виде суммы сферических гармоник, иногда называют рядом Лапласа.
Пусть 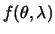 -- известная, кусочно-непрерывная функция, заданная в сферических координатах. Аппроксимацию этой функции зададим в виде конечного ряда, содержащего
-- известная, кусочно-непрерывная функция, заданная в сферических координатах. Аппроксимацию этой функции зададим в виде конечного ряда, содержащего 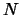 сферических гармоник
сферических гармоник
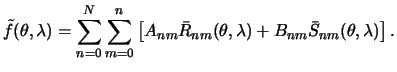
| (4.13) |
Определим коэффициенты этого разложения так, чтобы функция 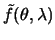 аппроксимировала функцию
аппроксимировала функцию 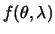 с наименьшим среднеквадратическим отклонением
с наименьшим среднеквадратическим отклонением
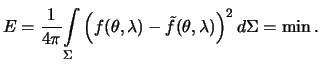
| (4.14) |
Для определения коэффициентов 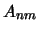 и
и 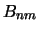 воспользуемся условиями
воспользуемся условиями

где 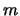 и
и 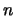 , заданные числа. Выполняя дифференцирование, с учетом (4.13), получим
, заданные числа. Выполняя дифференцирование, с учетом (4.13), получим
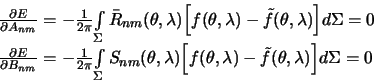
| (4.15) |
В полученные выражения нужно подставить вместо 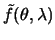 правую часть формулы (4.13), заменив в ней индексы суммирования
правую часть формулы (4.13), заменив в ней индексы суммирования 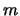 и
и 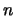 на
на 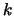 и
и 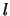 . Мы получим интегралы вида
. Мы получим интегралы вида
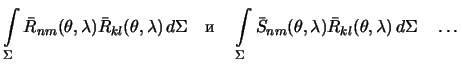
Вследствие ортогональности сферических гармоник только те из интегралов отличны от нуля, которые содержат произведения одноименных гармоник с одинаковыми индексами. Выполнив операции, получим
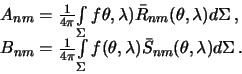
| (4.16) |
Итак, наилучшая средняя квадратическая аппроксимация функции 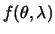 заданной на сфере, многочленом, составленным из нормированных сферических гармоник степени и порядка
заданной на сфере, многочленом, составленным из нормированных сферических гармоник степени и порядка 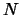 , имеет вид
, имеет вид
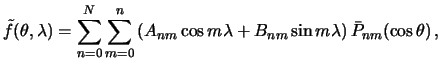
| (4.17) |
где 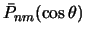 -- нормированная присоединенная функция Лежандра.
-- нормированная присоединенная функция Лежандра.
Специальное исследование показало, что наш ряд при неограниченном увеличении числа членов при некоторых дополнительных условиях, накладываемых на функцию 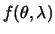 , сходится. Однако, исследование скорости этой сходимости лежит за пределами нашего курса.
, сходится. Однако, исследование скорости этой сходимости лежит за пределами нашего курса.
Date: 2015-09-05; view: 545; Нарушение авторских прав