Интегрирование дифференциального уравнения

Заменим переменную 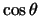на 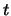. тогда 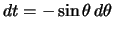. Очевидно, что

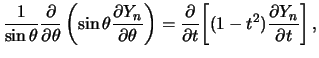
поэтому дифференциальное уравнение (3.20) можно переписать так

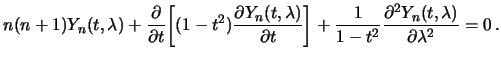
(3.21)

Будем искать решение этого уравнения в виде 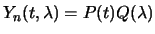. Подставив это выражение в дифференциальное уравнение, будем иметь

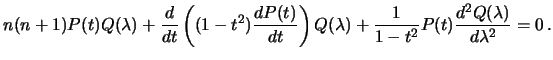
Умножив каждый член полученного выражения на 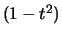и поделив на 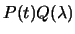, получим

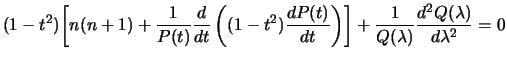
Видим, что первые два члена зависят только от 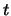, а последний -- только от 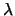Для того, чтобы уравнение выполнялось для любых 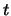и 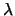, необходимо, чтобы эти функции выродились в константы. Например, уравнение будет выполняться, если

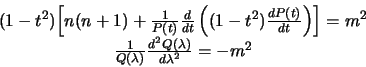
(3.22)

Второе уравнение есть уравнение гармонических колебаний

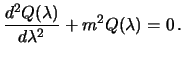
Его решение для любых действительных значений 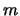имеет вид

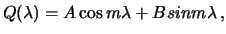
где 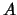и 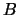-- постоянные интегрирования. Решение первого из приведенных выше уравнений, зависит как от постоянной 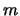, так и от постоянной 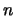. Обозначив решение через 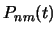, получим

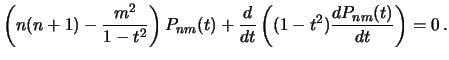
(3.23)

Функция 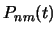при целочисленных значениях 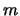носит название присоединенной (ассоциативной) функции Лежандра. В случае 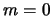, эти функции становятся степенными полиномами, которые называются полиномами Лежандра. Полагая в уравнении (3.23) 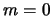, получим дифференциальное уравнение для полиномов Лежандра

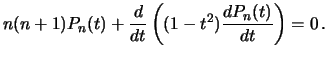
(3.24)

В теории специальных функций свойства функций и полиномов Лежандра достаточно хорошо изучены. Приведем лишь некоторые сведения (без вывода), которые могут пригодиться в нашем курсе. Присоединенные функции Лежандра и полиномы Лежандра связаны между собой соотношением

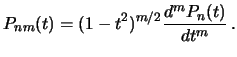
(3.25)

Подводя итог сказанному, выпишем окончательный вид решения дифференциального уравнения для сферических функций

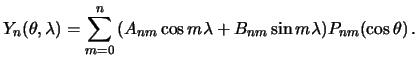
(3.26)

Заметим, что порядок производной 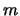в (3.25) не может быть больше степени 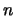полинома Лежандра. По этой причине постоянные 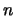и 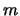называют степенью и порядком сферических функций.

Date: 2015-09-05; view: 493; Нарушение авторских прав