Ортогональность сферический функций

Ортогональность полиномов Лежандра определяется формулой

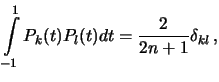
(4.3)

где 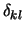-- символ Кронекера. Присоединенные функции Лежандра также обладают свойством ортогональности. Из теории специальных функций известно, что

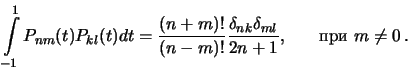
(4.4)

Сферические функции также образуют класс ортогональных функций. Докажем свойство ортогональности сферических функций. Возьмем две шаровые функции первого рода 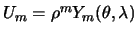и .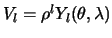

Применим к ним вторую формулу Грина для сферы. Учитывая, что 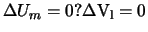, формула Грина принимает вид

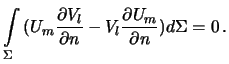
(4.5)

Для сферы производная по нормали совпадает с производной по радиус-вектору 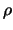, поэтому

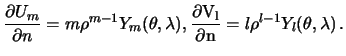
Подставляя полученные выражения в формулу (4.5), будем иметь

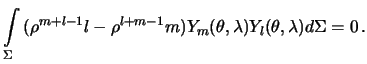
Поскольку радиус-вектор -- постоянная величина, полученное выражение можно переписать в следующем виде

(4.6)

При 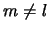приведенный интеграл равен нулю, что указывает на ортогональность сферических функций.

Вернемся теперь к сферическим функциям степени 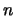, заданной в общем виде

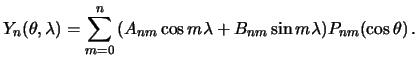
(4.7)

Функции вида

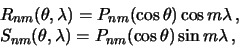
(4.8)

называются сферическими гармониками. Очевидно, что 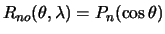, 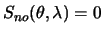. Можно показать, что

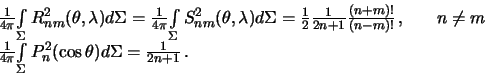
(4.9)

Все основные выкладки можно найти в учебниках по специальным функциям.

Date: 2015-09-05; view: 608; Нарушение авторских прав