Теорема Стокса

Эта теорема доказывает единственность внешней краевой задачи теории потенциала. Другими словами, если некоторое тело равномерно вращается с известной угловой скоростью, его поверхность, являющаяся поверхностью уровня, которая охватывает всю массу, также известна, то потенциал тяжести и его первые производные будут однозначно определены как на поверхности 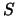, так и во всем внешнем пространстве.

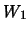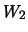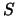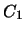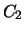Теорема доказывается от противного. Предположим, что существует два различных потенциала тяжести и , которые принимают на поверхности постоянные значения и . Таким образом, 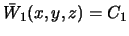, , 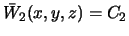где черта сверху означает, что значения функции относятся к поверхности 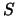. Поскольку потенциал тяжести есть сумма потенциала тяготения и центробежного потенциала, то

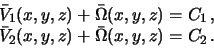
Обозначим разность 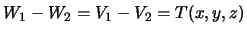. Полученная функция гармоническая, так как потенциал притяжения -- гармоническая функция, удовлетворяющая во внешнем пространстве уравнению Лапласа.

Применим первую формулу Грина (см. лекцию 3, раздел 3.1.2???) для случая, когда 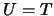и 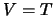. Выберем, в качестве "тела" по которому нужно выполнить интегрирование -- пространство, лежащее между поверхностью 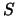и сферой 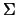с очень большим радиусом, так чтобы наша поверхность была целиком внутри сферы. Обозначим это пространство через 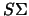. Теперь первая формула Грина будет выглядеть следующим образом

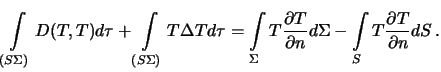
(6.7)

Знак минус между интегралами в правой части полученной формулы означает лишь то, что внешняя нормаль для одной поверхности является внутренней для другой поверхности. Рассмотрим последний интеграл. Функция 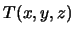на поверхности 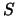-- постоянная величина, равная 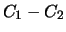, поэтому

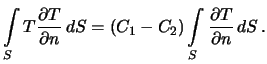
Однако, поскольку функция Т является гармонической, интеграл по замкнутой поверхности от нормальной производной, согласно теореме о потоке (см. лекцию 3, раздел 3.2.2), равен нулю.

Рассмотрим теперь второй интеграл в правой части выражения (6.7). Производная по нормали к сфере есть производная по радиус-вектору. Поскольку для очень большого радиуса исходное тело можно считать материальной точкой, то 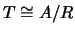. Аналогично 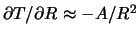, где 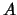-- постоянная величина. Отсюда следует

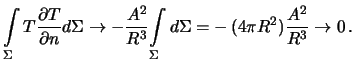
В левой части равенства (6.7) нужно положить 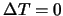, так как 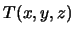-- функция гармоническая, поэтому это выражение принимает вид

Поскольку подынтегральное выражение не может быть отрицательным ни при каких значениях координат, остается сделать вывод, что 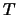-- постоянная величина во всем внешнем пространстве. Но на сфере с бесконечно большим радиусом она равна нулю и в силу непрерывности она равна нулю и на поверхности 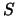. Таким образом T(x,y,z)=0 во всем внешнем пространстве, то есть 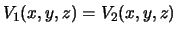, что и доказывает теорему.

Date: 2015-09-05; view: 531; Нарушение авторских прав