Дифференциальное уравнение для сферических функций

Поскольку шаровые функции удовлетворяют уравнению Лапласа, то есть

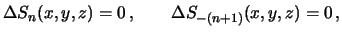
то должны выполняться и уравнения

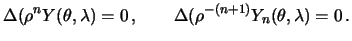
В последнем варианте шаровые функции записаны в сферических координатах, поэтому нам необходимо уравнение Лапласа переписать также в сферических координатах.

Из дифференциальной геометрии известно, что если 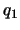, , 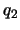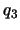-- обобщенные координаты, то элемент дуги в этой системе координат будет иметь вид

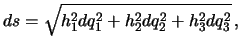
где 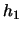, , 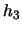-- коэффициенты Ламе:

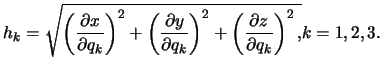
Теперь оператор Лапласа можно определить следующим образом (без вывода)

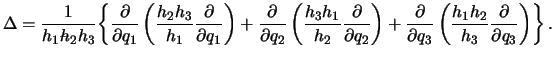
(3.18)

Определим коэффициенты Ламе для сферической системы координат. В данном случае 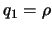, , , 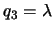поэтому

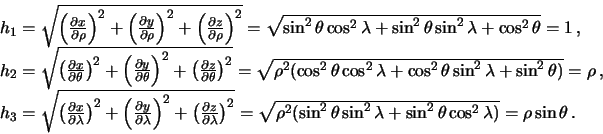
Оператор Лапласа для сферических координат будет выглядеть так

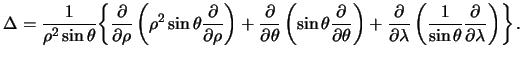
(3.19)

Применим этот оператор к шаровой функции вида 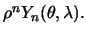Очевидно, что оператор Лапласа для шаровой функции равен нулю, поэтому

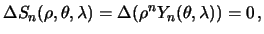
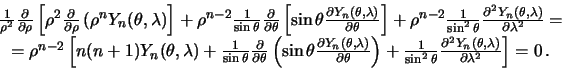
Таким образом, дифференциальное уравнение для сферической функции порядка 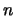имеет вид

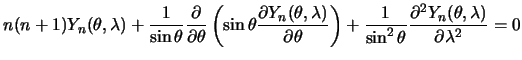
(3.20)

Предлагаем самостоятельно убедиться в том, что дифференциальное уравнение для функции входящую в шаровую функцию второго рода 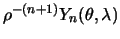совпадает с уравнением (3.20).

Date: 2015-09-05; view: 629; Нарушение авторских прав