Свойства гармонических функций

1. Линейная комбинация двух и более гармонических функций есть функция гармоническая.

Пусть U(x,y,z) и V(x,y,z) -- две гармонические функции, то есть 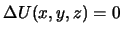и 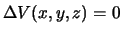. Возьмем их линейную комбинацию 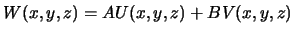. Очевидно, что 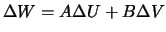. Поскольку 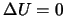, , 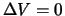то и 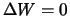, что и доказывает наше утверждение.

1. Если 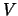-- гармоническая функция, то все ее частные производные гармонические функции. Доказательство основано на взаимной переставимости оператора Лапласа 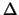и производных. Пусть

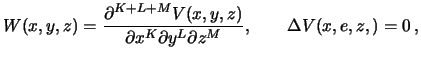
тогда

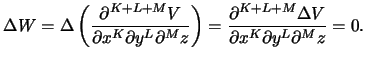
1. Линейное преобразование координат (поворот осей, изменение масштаба) не нарушает свойство гармоничности.

Пусть 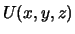-- гармоническая функция. Введем новые координаты

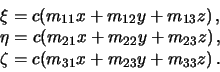
В матричном виде приведенное равенство выглядит следующим образом

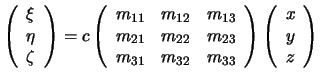
или

Подставим в функцию 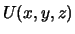линейные выражения для 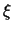, , 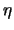, для чего воспользуемся вторым из приведенных выше равенств, получим V(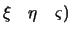. Докажем, что если 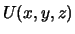функция гармоническая, то и 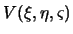является гармонической функцией.

Очевидно, что

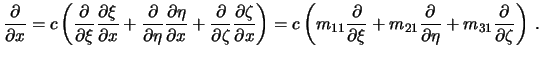
Аналогично

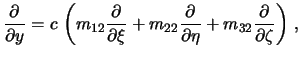
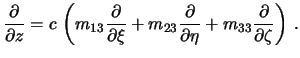
Запишем полученные равенства в матричной форме

Поскольку оператор Лапласа есть квадрат векторного оператора набла , то

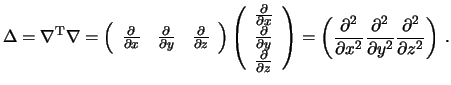
В правой части будем иметь

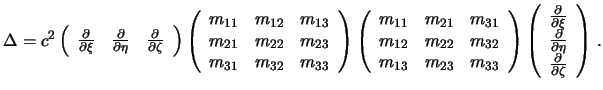
Поскольку матрицы направляющих косинусов являются ортонормированными, их произведения равны единичной матрице и оператор Лапласа принимает вид

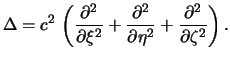
Отсюда следует, что оператор Лапласа является инвариантом по отношению к повороту осей, а при изменении масштаба множителем с изменяется на множитель . Другими словами, если 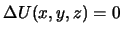, то .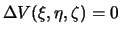

3.2.2 Теоремы о гармонических функциях

1. Теорема Гаусса: Поток градиента гармонической функции через замкнутую поверхность равен нулю. Потоком называется интеграл по заданной поверхности от нормальной производной функции.

Пусть 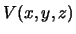-- гармоническая функция. Предположим, что задана замкнутая поверхность S, ограничивающая область, внутри которой эта функция -- гармоническая. Тогда, используя формулу Остроградского (3.1), получим

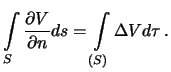
Но так как функция 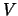гармоническая, то 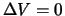, поэтому

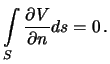
В случае, когда -- потенциал притяжения, то справедливо уравнение Пуассона 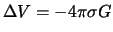, где 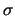-- плотность притягивающих масс. Тогда формула (3.1) приводит к формуле Гаусса.

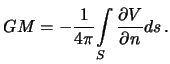
(3.11)

1. Гармоническая функция в замкнутой области D не имеет ни минимума, ни максимума.

Преположим обратное: внутри области 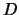существует точка , в которой гармоническая функция имеет максимум. В малой окрестности этой точки на сфере нормальная производная функции 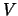будет отрицательной, тогда , что противоречит теореме Гаусса.

1. textitПотенциал притяжения вне притягивающих масс не может иметь ни минимума, ни максимума; внутри этой области может иметь только максимум.

Любая область вне притягивающего тела есть область определения гармонической функции, внутри которой, согласно теореме 2, не может иметь ни минимума, ни максимума. Предположим обратное: внутри притягивающего тела существует точка , в которой потенциал притяжения достигает минимума. В этой точке справедливо уравнение Пуассона . По формуле Остроградского будем иметь

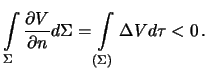
Mы пришли к противоречию: вследствие минимума внутри малой сферы, нормальная производная на поверхности этой сферы будет положительной, следовательно и приведенные выше интегралы будут положительны, что противоречит сделанному выше выводу. Таким образом, теорему можно считать доказанной.

1. Теорема Гаусса. Значение гармонической функции в центре сферы равно среднему из значений этой функции на поверхности.

Обратимся к третьей формуле Грина, когда точка внутренняя. Для гармонической функции 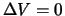, поэтому на сфере 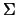формула (3.8) принимает вид

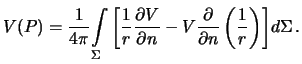
На поверхности сферы нормальная производная совпадает с производной по радиус-вектору, поэтому

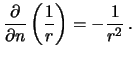
Кроме того, на поверхности сферы 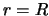, поэтому

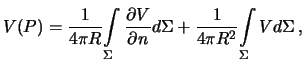
но согласно теореме Гаусса о потоке первое слагаемое в полученном выражении равно нулю, то есть

что и требовалось доказать.

Date: 2015-09-05; view: 1052; Нарушение авторских прав