Третья формула Грина

Рассмотрим частный случай, когда 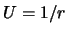, где 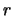-- расстояние между двумя точками P(x,y,z) и 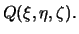Первая точка имеет фиксированные координаты, а вторая -- принадлежит телу и имеет текущие координаты, принадлежащие элементу объема. Тогда

Нетрудно убедиться, что для 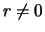, имеет место равенство 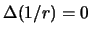. Имеем

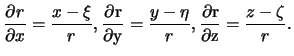
Проделаем следующие выкладки

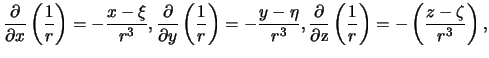
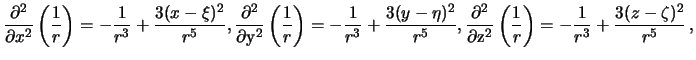
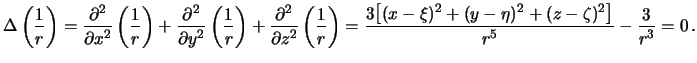
Обратимся снова к второй формуле Грина. Перепишем ее для случая, когда 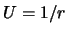. Возможны три варианта, когда точка лежит вне тела, внутри его и на поверхности, которое ограничивает это тело.

• Точка Р -- внешняя. В этом случае во всем внутреннем пространстве тела, по которому ведется интегрирование, радиус-вектор r не обращается в нуль и 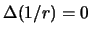. Вторая формула Грина (3.6) принимает вид

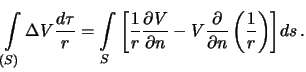
(3.7)

• 
  
• Мы получили третью формулу Грина для внешней точки.
• Точка Р -- внутренняя. В одной точке внутреннего пространства радиус-вектор обращается в нуль и функция обращается в бесконечность. Опишем вокруг этой точки сферу 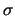с малым радиусом. Интегрирование по телу, ограниченному поверхностью 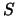, можно разбить на два этапа: интегрированию по всем точкам тела, исключая малую сферу, содержащую точку , и интегрирование по малому шару, ограниченному малой сферой :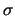

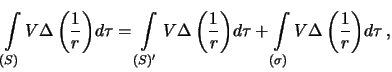
где 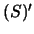-- тело с выколотой точкой . Поскольку 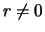во всем внутреннем пространстве 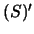, то первое слагаемое в правой части полученной формулы обращается в нуль, так как 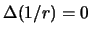. Займемся вторым слагаемым. Будем считать, что радиус малой сферы 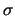настолько мал, что функцию 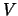внутри этой сферы -- постоянная величина. Тогда

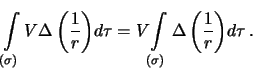
Воспользуемся формулой Остроградского, в которой положим 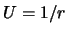, тогда вместо интегрирования по объему будем интегрировать по поверхности малой сферы

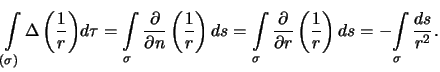
Отношение 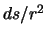есть элементарный телесный угол 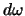, под которым "виден" из точки элемент поверхности сферы. Понятно, что, если точка находится внутри этой сферы, то рассматриваемый интеграл будет равен полному телесному углу, по которым видна поверхность сферы изнутри. Очевидно, что он равен 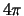, то есть

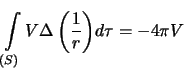
Перепишем формулу (3.6) в следующем виде

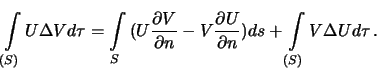
В случае 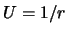, для внешней точки получим

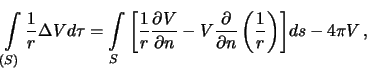
(3.8)

• Точка P лежит на поверхности. Третий случай -- это когда точка не является ни внутренней ни внешней: она лежит на поверхности тела. Можно показать, что в этом случае

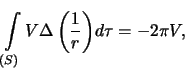
noindent поэтому третья формула Грина принимает вид

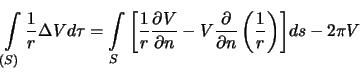
(3.9)

Формулы (3.7), (3.8) и (3.9) можно записать одной формулой

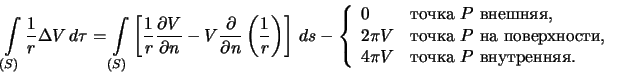
(3.10)

Date: 2015-09-05; view: 1105; Нарушение авторских прав