Метод, основанный на использовании векторного уравнения. Векторное уравнение для ускорений получается из следующей теоремы

Векторное уравнение для ускорений получается из следующей теоремы.

Ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки при вращении фигуры вокруг полюса, т.е.

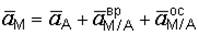, (3.10)

где 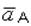– ускорение полюса А (см. рис. 3.17); 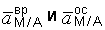– вращательное и осестремительное ускорение точки М при вращении плоской фигуры вокруг полюса А.

Осестремительное ускорение точки М при вращении вокруг полюса А в уравнении (3.10) направлено к полюсу (рис. 3.17), модуль его

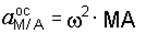, (3.11)

где w – мгновенная угловая скорость плоской фигуры.

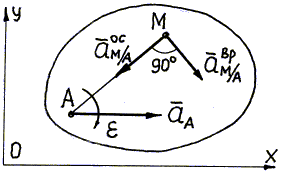Рис. 3.17.

Вращательное ускорение точки М при вращении вокруг полюса А направлено перпендикулярно осестремительному в сторону дуговой стрелки углового ускорения e и равно по модулю (рис. 3.17) 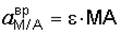, (3.12) где e – мгновенное угловое ускорение плоской фигуры.

Напомним, что при ускоренном вращении плоской фигуры вокруг полюса направление дуговой стрелки e совпадает с направлением вращения, а при замедленном вращении – противоположно ему.

С помощью уравнения (3.10) задача определения ускорений чаще всего решается для заданного момента времени. При решении задачи векторное уравнение (3.10) проектируется на оси координат. Для этого надо изобразить на чертеже все векторы, входящие в уравнение. Проектирование начинается с векторов (или вектора), стоящих в левой части векторного уравнения. Затем ставится знак равенства и проектируются векторы правой части уравнения. В результате одно векторное уравнение (3.10) заменяется двумя алгебраическими уравнениями проекций. Чтобы система алгебраических уравнений была разрешима, необходимо наличие в ней не более двух неизвестных величин. В качестве неизвестных могут быть любые две из следующих трех величин: одна или две составляющие ускорения точки А и угловое ускорение e плоской фигуры. Отметим, что угловая скорость w определяется заранее при решении задачи о скоростях.

Все вышесказанное позволяет рекомендовать следующую последовательность решения задачи определения ускорений.

1. Изобразить на чертеже положение тела в заданный момент времени, выбрать полюс и отметить точку, ускорение которой требуется определить. За полюс выбирается точка, ускорение которой либо известно по величине и направлению, либо легко определяется по условию задачи до решения уравнения (3.10).

2. Записать основное векторное уравнение (3.10) для точки, ускорение которой надо найти.

3. Показать на чертеже все векторы, входящие в уравнение (3.10). Если направление искомого вектора ускорения неизвестно, то его надо представить составляющими по направлению выбранных координатных осей.

4. Провести анализ уравнения (3.10), то есть выявить, какие величины в нем известны, а какие неизвестны. В результате анализа и предварительных вычислений в этом уравнении должно остаться не более двух неизвестных величин.

5. Спроектировать уравнение (3.10) на выбранные оси координат. Следить за тем, чтобы знак равенства сохранял свое место и в уравнениях проекций.

6. Решая полученную систему уравнений проекций, определить неизвестные величины.

В зависимости от того, какие неизвестные входят в основное векторное уравнение, задачи определения ускорений могут быть разделены на три основных типа.

Тип 1 – задача, в которой неизвестными уравнения (3.10) являются две составляющие ускорения рассматриваемой точки М. Это значит, ускорение полюса` а _А, угловая скорость w и угловое ускорение e должны быть заданы или определены по исходным данным до решения векторного уравнения (см. задачу 3.9).

Тип 2 – задача, возникающая при качении колеса без проскальзывания, когда задается скорость и ускорение центра колеса. Особенности кинематики колеса позволяют в этом случае определить угловую скорость и угловое ускорение колеса до решения векторного уравнения (см. задачу 3.10).

Тип 3 – задача, в которой неизвестными векторного уравнения (3.10) являются одна из составляющих ускорений рассматриваемой точки М и угловое ускорение тела e. В этих задачах, как правило, задается скорость и ускорение полюса А и траектория движения точки М (см. задачу 3.11).

Тип задачи окончательно может быть установлен только после анализа векторного уравнения (3.10). Однако в наиболее простых случаях само условие задачи, весь набор данных определяют заранее тип задачи и, следовательно, особенности ее решения.

Date: 2015-09-18; view: 437; Нарушение авторских прав