Задача 3.9 (16)

Равносторонний треугольник (рис. 3.18) со стороной 1 м движется в плоскости так, что ускорение его вершины А известно и равно а _А = 2 м/с², угловая скорость и угловое ускорение в данный момент времени соответственно равны 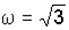1/с; 1/с². Определить ускорение вершины В треугольника.

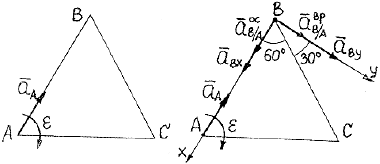
Рис. 3.18 Рис. 3.19

Решение

1. В качестве полюса выберем точку А, ускорение которой известно.

2. Для определения ускорения точки В запишем векторное уравнение типа (3.10)

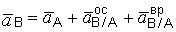. (а)

3. Изобразим все векторы, входящие в уравнение (а), на рис. 3.19. Ускорение точки В, неизвестное по направлению, представим составляющими` а <sub>Вх</sub> и` а _Ву; вектор` а _А ускорения полюса А задан условием задачи; осестремительное ускорение точки В при вращении вокруг полюса А направим от точки В к полюсу, его модуль

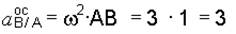м/с²;

вращательное ускорение точки В при вращении вокруг полюса А направим перпендикулярно осестремительному в сторону дуговой стрелки углового ускорения, его модуль равен

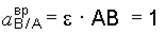м/с².

4. Анализ векторного уравнения (а) показывает, что задача относится к типу 1, так как неизвестными здесь являются обе составляющие ускорения точки В –` а <sub>Вх</sub> и` а _Ву.

5. Находятся они проектированием векторного уравнения (а) на координатные оси х и у. Отметим еще раз, что при проектировании векторного уравнения на оси, знак равенства в уравнении сохраняет свое место. В результате проектирования получим

(х) ;

(у) .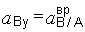

6. Отсюда находим неизвестные проекции ускорения точки В:

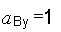м/с²;

м/с².

Эти проекции позволяют вычислить полное ускорение точки В

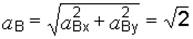м/с².

Date: 2015-09-18; view: 355; Нарушение авторских прав