Теорема об изменении момента количества движения системы

Для механической системы главным моментом количества движения относительно какой-либо точки О (или кинетическим моментом системы) называют векторную сумму моментов количества движения всех точек этой системы, взятых относительно точки О. Обозначая эту величину через.Ко, по определению имеем:

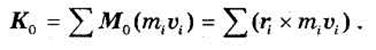
Здесь и далее суммирование распространяется на все N точек системы.

Используя формулы (32.22), запишем равенство (36.1) в проекциях на декартовы прямоугольные оси х, у, г:

где Кх, Ку, Кz — кинетические моменты системы относительно осей координат, хi:, yi, zi и v_xi, v_yi, v_zi — соответственно координаты и проекции вектора скорости i-й точки на координатные оси.

Чтобы усвоить механический смысл кинетического момента системы, вычислим его величину для твердого тела, вращающегося вокруг неподвижной оси Оz с угловой скоростью w По формулам (36.2) имеем:

Но при вращении тела вокруг оси Оz модуль скорости любой i-й точки равен v_i = hw, причем количество движения m_iv_i перпендикулярно отрезку h; опущенному из точки Ni на ось вращения. Вектор m_iv_i лежит в плоскости, нормальной к Oz. Следовательно, для любой точки тела момент количества движения относительно оси Oz будет:

Тогда для всего тела получим:

Но по определению (33.9) сумма в этой формуле есть момент инерции Jz тела относительно оси Oz. Таким образом, окончательно имеем:

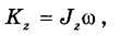
т. е. кинетический момент вращающегося тела относительно оси вращения равен произведению момента инерции тела относительно этой оси на угловую скорость тела.

Если к точкам системы приложить все внешние и внутренние силы и обозначить равнодействующую внешних и внутренних сил, прилагаемых к k-я точке, соответственно через F^e_k и Fⁱ_k, то на основании теоремы (32.24) для k-й точки, можем записать:

Составляя такие уравнения для всех точек системы и складывая их левые и правые части, получим:

Но по свойству внутренних сил (34.4) последняя сумма равна нулю. Поэтому окончательно имеем:

Полученный результат выражает следующую теорему моментов: производная по времени от кинетического момента системы относительно какой-либо точки равна геометрической сумме моментов внешних сил, действующих на систему, относительно той же точки.

В проекциях на оси декартовой прямоугольной системы координат Oxyz равенство (36.4) имеет вид:

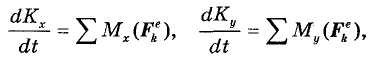
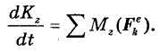
Следствие 1. Пусть сумма моментов всех внешних сил относительно точки О равна нулю, т. е.

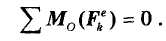
В этом случае из теоремы (36.4) вытекает, что

Таким образом, если сумма моментов всех приложенных к системе внешних сил относительно некоторой точки равна нулю, то кинетический момент системы относительно этой точки остается неизменным как по величине, так и по направлению.

Следствие 2. Пусть сумма моментов всех внешних сил относительно некоторой оси, например Ох, обращается в нуль. Тогда из формул (36.5) следует, что при этом Кх = const, т. е. если сумма моментов всех действующих на систему внешних сил относительно какой-либо оси равна нулю, то кинетический момент системы относительно этой же оси есть величина постоянная.

Сформулированные следствия выражают закон сохранения кинетического момента системы. Согласно этому закону, внутренние силы не могут изменить главный момент количества движения системы.

Теорема об изменении кинетического момента позволяет получить дифференциальное уравнение вращения тела вокруг неподвижной оси. Пусть, например, Oz — ось вращения тела. По формулам (36.5) и (36.3) имеем

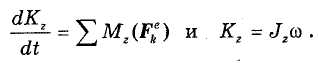
Отсюда для неизменяемой системы получим:

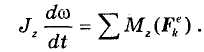
Выражая угловую скорость через угол поворота j, имеем:

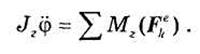
Зависимость (36.6) представляет дифференциальное уравнение вращательного движения тела вокруг неподвижной оси.

ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ

Кинетической энергией (Т) механической системы называется сумма кинетических энергий всех ее точек, т.e.

где m_k и v_k — соответственно масса и скорость k-й точки, а суммирование распространяется на все точки системы. Из определения следует, что кинетическая энергия системы может быть равна нулю только в том случае, когда все ее точки находятся в покое.

Вычислим кинетическую энергию при различных случаях движения системы.

При поступательном движении все точки системы, включая центр масс С, движутся с одинаковыми скоростями, так что v_k= v_c для всех k и из формулы получим:

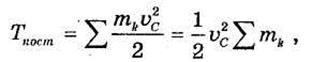
или

где М — масса системы.

В случае вращательного движения системы вокруг какой-нибудь оси Oz с угловой скоростью w имеем: v_k = wh_k, где h_k — расстояние точки от оси вращения. Тогда для кинетической энергии (Т_вр) получим:

или,

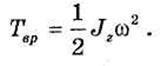
В общем случае движения скорость произвольной точки системы можно представить в виде суммы скорости центра масс v_c, принимаемого за полюс, и скорости v’_k k-й точки при вращательном движении с угловой скоростью со вокруг мгновенной оси СР, т.е.

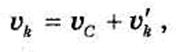
причем модуль вектора v'k равен v'k =wh_k. Тогда:

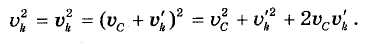
Подставляя этот результат в формулу (37,1), получим:

Учитывая, что первая сумма есть масса системы М, вторая сумма — момент инерции системы относительно мгновенной оси СР, а третья сумма, представляющая собой количество движения системы при вращении вокруг оси СР, проходящей через центр масс, равна нулю, получим в общем случае движения системы:

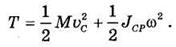
Рассматривая теорему об изменении кинетической энергии точки как какую-либо k-ю точку системыможем записать:

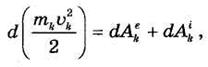
где dA^e_k и dA^l_k — элементарные работы приложенных к k точке внешних и внутренних сил. Составляя такие соотношения для всех точек системы и складывая их почленно, получим:

или

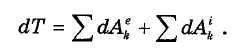
Полученное равенство выражает теорему об изменении кинетической энергии системы в дифференциальной форме: дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему.

Проинтегрировав обе части равенства (37.5) между двумя положениями системы — начальным и конечным, в которых кинетическая энергия равна соответственно То и T₁, получим:

Формула выражает в конечной (или интегральной) форме теорему об изменении кинетической энергии системы: изменение кинетической энергии системы при ее перемещении из одного положения в другое равно сумме работ всех внешних и внутренних сил, приложенных к системе, на соответствующих перемещениях точек системы при том же ее перемещении.

В случае неизменяемой системы (абсолютно твердое тело) сумма работ внутренних сил равна нулю:

Следовательно, для такой системы формулу можно представить в виде:

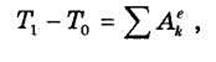
т. е. изменение кинетической энергии абсолютно твердого тела при каком-либо перемещении равно сумме работ всех действующих на тело внешних сил на перемещениях точек их приложения.

Date: 2015-09-03; view: 596; Нарушение авторских прав