Геометрия масс

Рассмотрим Механическую систему, состоящую из конечного числа N материальных точек с массами m₁, m₂,..., m_n, радиус-векторы которых, проведенные из одной и той же точки О, обозначим через r1, r2,..., r_n. Центром масс системы называется геометрическая точка С, радиус-вектор которой определяется формулой:

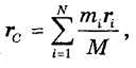
где М — масса системы.

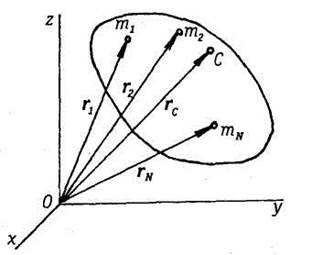
Обозначая декартовы координаты составляющих систему материальных точек через (x1, y1, z1), (x2, y2, z2). •••(x_n,y_n,z_n) и проектируя векторное равенство (33.1) на оси координат, получим формулы для определения координат центра масс:

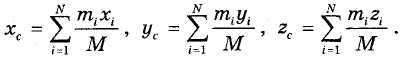
Из определения (33.1) следует, что центр масс является не материальной, а геометрической точкой, которая может не совпадать ни с одной материальной точкой системы (например, в случае кольца).

Вектор

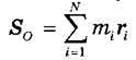
называется статическим моментом системы относительно точки О.

Скалярные величины

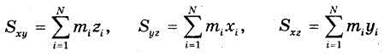
называются статическими моментами системы относительно плоскости О_ху, O_yz и O_xz соответственно.

Радиус-вектор и координаты центра масс системы выражаются через статические моменты по формулам:

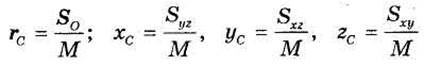
Пусть механическая система представляет собой сплошное тело. Разобьем его на бесконечно малые частицы с массами dm и изменяющимся от частицы к частице радиус-вектором г. Заменяя в формулах (33.1)—(33.3) суммы соответствующими интегральными суммами, в пределе получим:

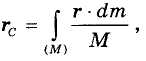
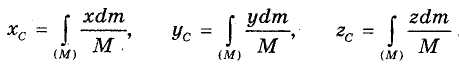
В случае однородного сплошного тела dm = rdV, М = rV, причем r — плотность тела, dV — объем элементарной частицы, а V — объем всего тела. Для тела типа тонкого листа, которое можно принять за материальную поверхность, dm = r_sds, M = r_sS, где r_s - поверхностная плотность, a S — площадь поверхности. Для тонкой проволоки, которую можно принять за отрезок материальной линии, dm = r_ldl, M = r_ll, где r_l — линейная плотность, dl — длина элемента линии и l — длина отрезка линии.

Для описания вращательных движений тела в динамике используются специальные геометрические характеристики распределения масс.

Моментом инерции механической системы из N материальных точек относительно точки О называется сумма произведений масс этих точек на квадраты их расстояний до точки О, т. е.

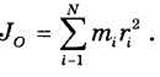
Момент инерции относительно точки часто называют также полярным моментом инерции. В случае сплошного тела операция суммирования заменяется интегрированием по области (М), занятой телом:

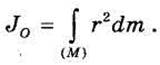
Моментом инерции J l системы из N материальных точек относительно оси l называется сумма произведений масс этих точек на квадраты их расстояний di до оси l, т. е.

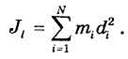
В случае сплошного распределения масс по аналогии с формулой (33.8) имеем:

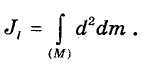
Если l — одна из декартовых осей х, у или z, то из определений (33.8)-(33.10) получим: для системы N материальных точек:

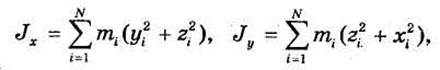
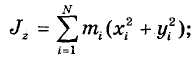
для сплошного тела:

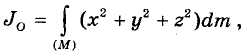
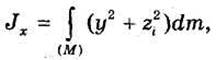
Из формул (33.13) и (33.14) вытекает, что

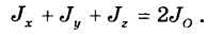
Равенство (33.15) выполняется для любых декартовых осей, проходящих через точку О. Это означает, что сумма моментов инерции не зависит от ориентации декартовых осей в рассматриваемой точке, т. е. является величиной инвариантной по отношению к направлению осей координат.

Центробежным моментом инерции системы N материальных точек относительно взаимно-ортогональных осей n и l называется величина

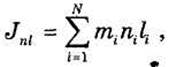
где ni, li — координаты i-й точки в осях nl.

Если n и l последовательно совмещать с декартовыми осями хуz, то получим три центробежных момента инерции:

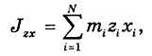
или, в случае сплошного тела:

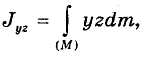
Оси, относительно которых центробежные моменты тела обращаются в ноль, называются главными осями инерции. Главные оси, проходящие через центр масс тел, называются главными центральными осями.

Моменты инерции относительно параллельных осей. Пусть имеем две системы прямоугольных, взаимно параллельных осей координат Oxyz и Сх'у'г'. Начало системы координат Сх'у'г' находится в центре масс сиcтемы (рис. 4.2.). Обозначим через d расстояние между осями Cz' и Oz. По формулам (33.12) имеем:

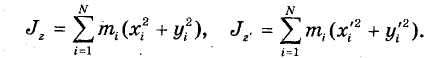
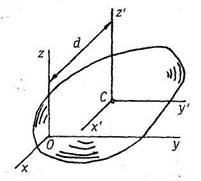
Но, как видно из рисунка (4.2.), для любой точки тела:

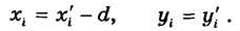
Тогда:

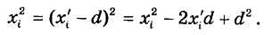
Подставляя эти значения в формулу для Jz, получим:

В правой части этого равенства первая сумма равна моменту инерции Iz. относительно оси Cz', вторая сумма есть масса системы М, а третья сумма, согласно первой из формул (32.2), может быть представлена как произведение Мх'с. Но ось х' проходит через центр масс и, следовательно, х'с — 0. Поэтому окончательно имеем:

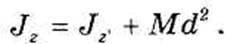
Полученная формула выражает теорему Штейнера: момент инерции тела относительно данной оси равен моменту инерции относительно параллельной ей центральной оси, сложенному с произведением массы тела на квадрат расстояния между осями.

Моменты инерции некоторых однородных тел. Во многих задачах механики моменты инерции тел сложной формы часто удается вычислить путем разбиения тела на несколько тел простой формы. Моменты инерции сложных тел получают суммированием моментов инерции частей этих тел.

Однородный стержень.

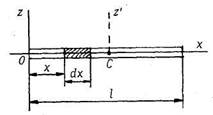
Подсчитаем момент инерции стержня относительно центральной оси Сz'; параллельной Оz. Используя формулу (33.19), получим:

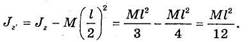
Следовательно,

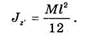
Прямоугольная пластинка.

Для центральной оси у' получим из формулы (33.19):

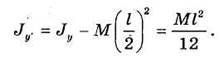
момент инерции пластинки относительно оси Ох:

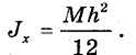
Круговая шайба.

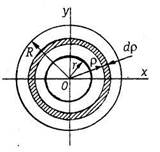
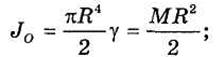
где М— масса сплошной круглой пластинки.

Круглый однородный цилиндр.

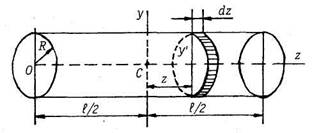
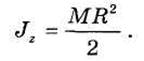
момент инерции цилиндра относительно центральной оси Су, перпендикулярной оси цилиндра.

ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ

Рассмотрим механическую систему, состоящую из N материальных точек. Пусть на какую-нибудь k-ю точку системы с массой m_k действуют внешние (активные и реактивные) силы с равнодействующей F^e_k и внутренние силы, равнодействующую которых обозначим через Fⁱ_k;

Согласно основному закону динамики, ускорение точки a_k связано с действующими силами зависимостью:

т. е.

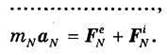
Складывая левые и правые части равенств (34.1), имеем:

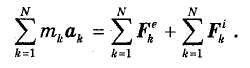
Проанализируем полученное равенство. Во-первых, по формуле (33.1) можем записать:

где r_k — радиус-вектор k-й точки системы, М — ее масса, а r_с — радиус-вектор центра масс. Дважды дифференцируя это равенство по времени, найдем:

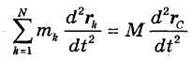
или

причем а_с — ускорение центра масс системы.

Во-вторых, согласно третьему закону Ньютона, любые две точки j и k системы взаимодействуют равными по модулю и противоположно направленными силами. Fⁱ_jk и Fⁱ_kj, сумма которых равна нулю. Поэтому для всех точек системы равнодействующая внутренних сил обращается в нуль, т. е.

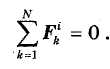
Подставляя результаты (34.3) и (34.4) в равенство (34.2), получим:

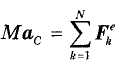
Уравнение (34.5) выражает теорему о движении центра масс системы: произведение массы механической системы на ускорение ее центра масс равно векторной сумме всех внешних сил, приложенных к системе.

Следствие 1. Если равнодействующая всех внешних сил, приложенных к системе, равна нулю, то центр масс этой системы движется равномерно и прямолинейно.

Это положение известно как закон сохранения движения центра масс.

Следствие 2. Если сумма проекций всех действующих на систему сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту же ось есть величина постоянная.

Для доказательства запишем векторное равенство (34.5) в проекциях на оси декартовой системы прямоугольных координат Oxyz. Получим три скалярных равенства:

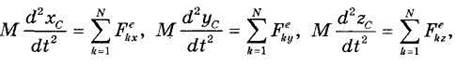
где х_с, у_с и z_с — координаты центра масс системы, а F_kx, F_ky, F_kz — проекции k-й силы на соответствующую ось.

ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ

Количеством движения механической системы, состоящей из N материальных точек, называется векторная величина Q, равная геометрической сумме количеств движения всех точек системы:

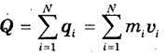
Запишем:

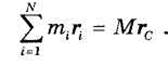
Дифференцируя обе части этой формулы по времени, получим при неизменных массах:

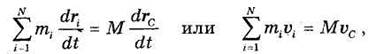
т. е.

Таким образом, количество движения системы равно произведению массы всей системы на скорость ее центра масс. Из этого определения вытекает, что при неподвижном центре масс количество движения системы равно нулю. В частности, при вращении твердого тела вокруг неподвижной оси, проходящей через центр масс, количество движения тела равно нулю. При сложном движении тела величина Q характеризует только поступательную часть движения. Например, для катящегося колеса Q = mv_c и не зависит от того, вращается колесо вокруг центра масс С или нет.

Запишем дифференциальное уравнение движения системы, состоящей из N материальных точек. Согласно закону (34.2), имеем:

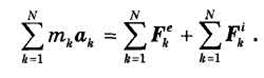
По свойству суммы внутренних сил

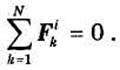
Кроме того:

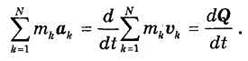
Таким образом, окончательно имеем:

Уравнение (35.3) в дифференциальной форме выражает теорему об изменении количества движения системы: производная по времени от количества движения системы равна главному вектору всех действующих на систему внешних сил.

В проекциях на декартовы прямоугольные оси Oxyz векторное уравнение (35.3) дает:

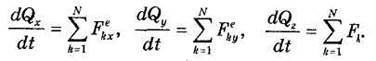
Получим другое выражение теоремы. Пусть в некоторый момент времени t₀ = 0 количество движения системы равно Qo, а в момент t₁ > t0 — Q₁. Интегрируя уравнение (35.3) в пределах от t₀ = О до t₁ получим:

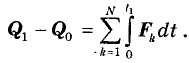
Но, согласно определению (32.4), интегралы в правой части представляют собой импульсы внешних сил. Поэтому:

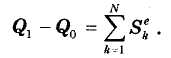
Полученное равенство выражает теорему об изменении количества движения системы в интегральной форме: изменение количества движения системы за конечный промежуток времени равно сумме импульсов приложенных к системе внешних сил за тот же промежуток времени.

В проекциях на координатные оси векторное равенство (35.5) эквивалентно трем скалярным уравнениям:

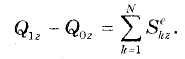
Следствие 1. Пусть главный вектор внешних сил, действующих на систему, равен нулю: 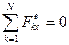. Тогда из уравнения (35.3) получаем, что Q = const.

Таким образом, если векторная сумма всех внешних сил, приложенных к системе, равна нулю, то вектор количества движения системы не изменяется ни по модулю, ни по направлению.

Следствие 2. В том случае, если сумма проекций всех внешних сил системы на какую-нибудь ось (например Ох) равна нулю, согласно формулам (35.4) получаем:

Qx= const при .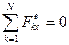

Результаты, выраженные следствиями 1 и 2, называют законом сохранения количества движения системы, который можно также сформулировать в виде: внутренние силы не могут изменить количества движения механической системы.

Date: 2015-09-03; view: 811; Нарушение авторских прав