Движение несвободной материальной точки

Основной закон динамики точки справедлив и для случая, когда на движущуюся точку наложены связи. При этом, конечно, могут возникнуть особенности решения первой и второй задач динамики, поскольку реактивные силы заранее неизвестны и их надо определить по заданным связям

Пусть связь представляет собой поверхность какого-либо тела, по которой движется точка. Тогда координаты точки должны удовлетворять уравнению этой поверхности, называемому уравнением связи

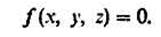
Аналогично, если точка вынуждена двигаться по некоторой линии (движение шарика внутри криволинейной трубки), то уравнениями связи являются уравнения этой линии

Таким образом, движение несвободной материальной точки зависит не только от приложенных к точке активных сил и начальных условий, но также от имеющихся связей. При этом значения начальных условий должны удовлетворять уравнениям связей.

Для такой несвободной материальной точки дифференциальные уравнения имеют тот же вид, что и для свободной точки, только к действующим силам надо добавить силы реакций связей.

Связей на двусторонние, или удерживающие, и на односторонние, или неудерживающие, связи.

Связь называется двусторонней, если накладываемые ею на координаты точки ограничения выражаются в форме равенств, определяющих кривые или поверхности в пространстве, на которых должна находиться эта точка.

Двусторонняя, или удерживающая, связь препятствует перемещению точки тела в двух противоположных направлениях.

Ограничения, накладываемые на координаты точки односторонней связью, выражаются неравенствами.

Последовательность решения задачи динамики несвободной точки проследим на примере движения точки по гладкой поверхности.

Пусть гладкая неподвижная поверхность задана уравнением f(x, у, z) = 0, причем х, у, z — координаты движущейся точки массой m под действием заданной силы F. Обозначим через N{N_X, Ny, Nz,} неизвестную нормальную силу реакции гладкой поверхности и запишем дифференциальные уравнения движения точки по поверхности:

В дифференциальной геометрии доказывается, что направляющие косинусы внешней нормали к поверхности, а следовательно и вектора N, вычисляются по формулам:

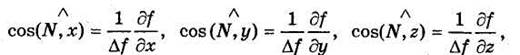
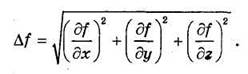
Тогда проекции вектора N на координатные оси можно выразить следующим образом:

где обозначено l= N/Df. Подставляя проекции в уравнения движения, получим:

Уравнения называют дифференциальными уравнениями Лагранжа первого рода. Эти три уравнения движения вместе с уравнением поверхности f{x,y,z)=0 позволяют найти четыре неизвестных — координаты точек х, у, z и неопределенный множитель Лагранжа l как функции времени и произвольных постоянных интегрирования. Последние определяются из начальных условий. После нахождения множителя l. легко определить силу нормальной реакции поверхности, модуль которой равен N = lDf, а направляющие косинусы выписаны ранее. В общем случае реактивная сила N будет зависеть от времени.

Date: 2015-09-03; view: 2016; Нарушение авторских прав