Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси

Вращение твердого тела вокруг его главной центральной оси инерции

Рассмотрим твердое тело, вращающееся вокруг неподвижной оси z под действием приложенных к нему внешних задаваемых сил Pi, Щ-, ••-, РЦ (Рис- 227,в). Предположим, что в рассматриваемый момент тело имеет угловую скорость ш и угловое ускорение е. Чтобы воспользоваться принципом Германа — Эйлера - Даламбера, приложим к каждой точке тела Mt силу инерции Ф,.

При неравномерном вращении тела эта сила состоит из вращатель­ной силы инерции Ф', направленной противоположно вращательному ускорению точки Mh и центробежной силы инерции Ф", направленной противоположно центростремительному ускорению этой точки. Приме­няя принцип освобождаемое! и от связей (см. § 21), заменяем действие на тело подпятника А и подшипника В реакциями &л и Й.в, разложив их на составляющие XА, YA, tA, XB, Тв-

Расстояние АВ между опорами тела обозначим h. На основании принципа Германа — Эйлера — Даламбера внешние задаваемые силы, реакции связей и силы инерции должны удовлетворять уравнениям (108.3) и (108.5), которые в данном случае принимают вид

Первому уравнению (110.1) соответствуют три уравнения проекций внешних задаваемых сил, реакций связей и сил инерции на оси коор­динат. Второму уравнению (110.1) соответствуют три уравнения момен­тов этих же сил относительно осей координат. Таким образом, всего имеем шесть следующих уравнений:

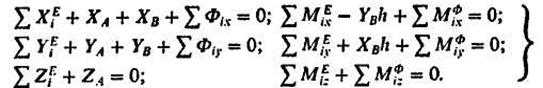
Установим формулы для вычисления сумм проекций сил инерции на оси координат и их моментов относительно этих осей.

Модули центробежной и вращательной сил инерции определим по формулам (2.10):

где rt — радиус окружности, описываемой точкой.

Разложим каждую из этих сил на составляющие, направленные по осям координат (рис. 227, б). Найдем алгебраические значения этих составляющих, т. с. проекции сил Ф', и 4>? на оси координат:

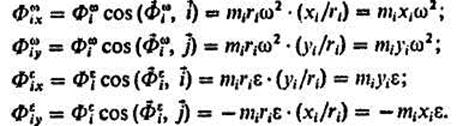
Найдем суммы проекций сил инерции на оси хну, пользуясь равенствами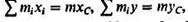

Найдем суммы моментов сил инерции относительно осей хну как суммы моментов центробежных и вращательных сил инерции:

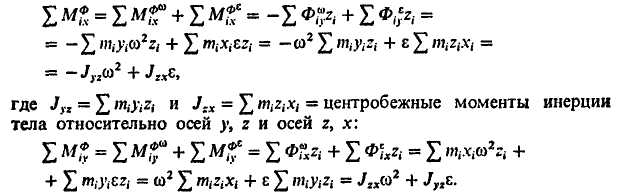
Учитывая, что центробежные силы инерции пересекают ось г, най­дем сумму моментов сил инерции относительно оси z как сумму моментов только вращательных сил инерции, не разложенных на

составляющие:

Подставим найденные значения в уравнения (110.2):

Последнее из уравнений (110.3) не содержит реакций опор. Это уравнение представляет собой дифференциальное уравнение вращения тела (79.2). Остальные пять уравнений позволяют определить пять составляющих реакций подпятника А и подшипника В.

В первое, второе, четвертое и пятое уравнения (U0.3), из которых определяются составляющие реакций опор вдоль осей хну, входят члены, зависящие как от внешних задаваемых сил, так и от сил инер­ции. Следовательно, каждая из этих реакций имеет статическую состав­ляющую, вызываемую действием внешних задаваемых сил Р[; и дина­мическую составляющую, зависящую от сил инерции. Члены уравне­ний (110.3), зависящие от сил инерции, отмечены рамками. При быст­ром вращении тела динамические составляющие могут иметь большие значения.

Установим условия, при которых динамические составляющие реакций подпятника и подшипника равны нулю. Чтобы получить' эти условия, приравняем нулю сумму членов, зависящих от сил инерции, в каждом из уравнений (110.3):

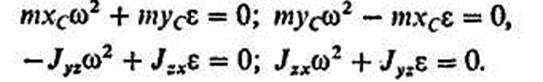
Решаем систему уравнений (110.4) относительно хс и ус:

т. е. устанавливаем, что центр тяжести тола должен находиться на оси его вршцения.

Решаем систему уравнений (110.5) относительно J,, и J,x:

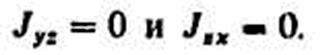
Это означает, что ось вращения тела г должна быть главной осью инерции тела для начала координат.

Таким образом, установлено, что динамические составляющие реак­ций подпятника и подшипника равны нулю в том случае, если ось вращения тела является главной центральной осью инерции тела.

Для выполнения этого условия вращающимся частям машин обычно придают форму тел вращения, с тем чтобы это тело вращалось вокруг своей оси симметрии. Если из-за неточности изготовления ось враще­ния тела не окажется главной центральной осью инерции, то эта погрешность устраняется специальными приемами.

Date: 2015-09-03; view: 3528; Нарушение авторских прав