
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Принцип Даламбера
|
|
Принципом Даламбера называется общий метод, при помощи которого уравнениям динамики придается вид уравнений статического равновесия.
Рассмотрим материальную точку М массы т, движущуюся под действием сил F1 F2,..., Fn с ускорением а. основное уравнение динамики точки имеет вид:
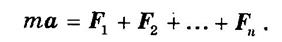
Обозначим Ф = —mа и перенесем все слагаемые в правую часть. Получим:
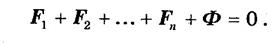

Сила Ф. равная произведению массы точки на ее ускорение и направленная противоположно ускорению, называется силой инерции.
Равенству можно дать такую трактовку: если в каждый момент времени к фактически действующим на точку силам прибавить силу инерции, то полученная система сил будет уравновешенной. Это положение, эквивалентное второму закону Ньютона, выражает принцип Даламбера.
Повторяя приведенные выше рассуждения к каждой из точек механической системы, мы придем к принципу Даламбера для системы: если в каждый момент времени ко всем точкам системы кроме фактически действующих внешних и внутренних сил приложить соответствующие силы инерции, то полученная система сил будет уравновешенной и к ней можно будет применять все уравнения статики.
Следует иметь в виду, что приложение сил инерции к системе (точке) является лишь формальным приемом, сводящим задачу динамики по форме решения к задаче статики.
Из статики известно, что для равновесия необходимо обращение в нуль геометрической суммы всех действующих на систему сил, а также суммы их моментов относительно произвольного центра О. Тогда на основании принципа Даламбера должно быть:
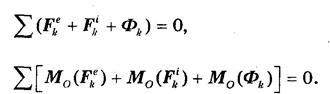
Обозначим:
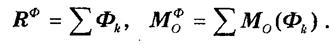
Величины Rф и Мфо называются соответственно главным вектором и главным моментом сил инерции относительно центра О. Учитывая, что для внутренних сил системы главный вектор и главный момент относительно центра О обращаются в нули, из равенств получим:
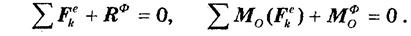
Уравнения не содержат внутренних сил, что во многих случаях упрощает процесс решения задач.
Date: 2015-09-03; view: 633; Нарушение авторских прав