
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Две основные задачи динамики точки
|
|
Дифференциальные уравнения динамики материальной точки в той или другой системе координат позволяют решать две основные задачи.
Первая задача. Известна масса точки и закон ее движения. Найти действующую на точку силу. Если, например, заданы уравнения движения в декартовой системе координат:

то из уравнений определяются проекции равнодействующей F на оси координат:

При известных проекциях Fx, Fy, Fz силы F легко определить ее модуль и направление.
Вторая задача. Известна масса точки и равнодействующая приложенных к ней сил. Найти закон движения этой точки. Рассмотрим решение поставленной задачи в прямоугольной декартовой системе координат. Сила F, вообще говоря, может зависеть от времени, координат движущейся точки, ее скорости, ускорения и т. д. Для простоты ограничимся случаем, когда сила F зависит лишь от времени, положения в пространстве и скорости точки. При этом предположении дифференциальные уравнения можно записать в виде:
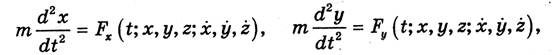

Таким образом, задача сводится к интегрированию системы трех обыкновенных дифференциальных уравнений второго порядка.
Date: 2015-09-03; view: 538; Нарушение авторских прав