
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Системы единиц
|
|
Основной закон динамики связывает между собой ускорение, силу и массу материальной точки. Размерность ускорения зависит от выбора единиц длины и времени. В силу закона единицы измерения длины, времени, массы и силы не могут быть выбраны независимо друг от друга. Независимыми являются только три из этих величин, размерность же четвертой определяется законом.
В международной системе СИ за единицу времени принята секунда (с), длины — метр (м), массы — килограмм (кг). За единицу силы здесь принимается ньютон (Н), равный силе, которая сообщает телу массой 1 кг ускорение, равное 1 м/с2.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
Из кинематики известно, что ускорение а выражается через радиус-вектор r материальной точки по формуле:

Подставляя эту зависимость в формулу (29.4), получим дифференциальное уравнение движения материальной точки в векторной форме:

Обозначая равнодействующую всех заданных сил и сил реакций связей через F, запишем уравнение в виде:

Если спроектировать обе части уравнения на оси декартовой прямоугольной системы координат Qxyz, получим:
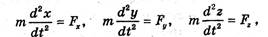
где х, у, z — проекции радиус-вектора r на оси х, у и z соответственно, a Fx, Fy, Fz – проекции равнодействующей F на указанные оси. Равенства представляют дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат.
Иногда удобнее рассматривать движение материальной точки в естественных подвижных осях координат. Проектируя обе части формулы (29.1) на естественные оси, получим:
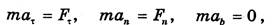
где аt, аn, аb и Ft, Fn, Fb — соответственно проекции ускорения и равнодействующей сил на касательную, главную нормаль и бинормаль к траектории точки в данный момент времени. В кинематике было установлено, что в естественных осях компоненты вектора ускорения выражаются через дуговую координату s, скорость точки и и радиус кривизны траектории р по формулам:

Подставляя эти зависимости в формулы (29.10), получим дифференциальные уравнения движения материальной точки в проекциях на естественные координатные оси:
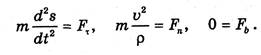
Date: 2015-09-03; view: 482; Нарушение авторских прав