Плоскопараллельное движение твердого тела

Как известно из кинематики, плоскопараллельным движением твердого тела называется такое движение, при котором расстояние каждой точки тела от данной неподвижной плоскости остается постоянным и при котором, следовательно, все точки тела движутся в плоскостях, параллельных этой неподвижной плоскости.

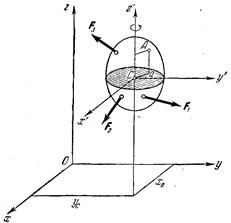
Предположим, что данное твердое тело движется параллельно некоторой неподвижной плоскости, которую примем за координатную плоскость хОу, под действием системы сил F₁, F₂,..., F_n).

Из кинематики известно также, что при плоскопараллельном движении положение твердого тела определяется тремя пара метрами: двумя координатами какой-нибудь точки этого тела и углом его поворота вокруг оси, проходящей через эту точку и перпендикулярной к той неподвижной плоскости, параллельно которой движется данное тело. Будем определять положение движущегося тела координатами х_с и у_с его центра тяжести и углом поворота φ вокруг оси z', проходящей через центр тяжести С и параллельной оси z₁). Для определения плоскопараллельного движения тела мы должны найти выражения этих трех параметров х_с, у_с и φ в функциях времени t, для чего необходимо составить три дифференциальных уравнения.

Воспользуемся теоремой о движении центра масс

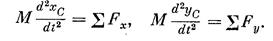
где М — масса данного тела.

Решение данных дифференциальных уравнений даст соответственно зависимости х_с=f(t), у_с=f(t).

Для определения последней зависимости проведем через центр тяжести С, кроме оси z', параллельной оси z, еще две другие координатные оси х' и у', предполагая, что эти оси остаются все время параллельными неподвижным осям x и y, так что движение подвижной системы осей Cx'y'z', т. е. переносное движение, будет поступательным. Тогда относительным движением данного тела, т. е. движением его относительно подвижной системы осей Cx'y'z', будет вращение вокруг оси Cz'.

Как известно из кинематики, ускорение a каждой точки тела при плоскопараллельном движении равно векторной сумме двух ускорений: 1) переносного ускорения этой точки, равного ускорению какой-нибудь точки тела, выбранной за начало подвижной системы осей, т. е. в рассматриваемом случае равного ускорению a_c точки С, и 2) относительного ускорения a_r этой точки, т. е. в данном случае ее ускорения во вращательном движении вокруг оси Cz'. Это относительное ускорение a_r складывается в свою очередь из двух ускорений — нормального a_{r n} и касательного a_rτ. Следовательно,

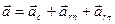
Воспользуемся принципом Даламбера для системы.

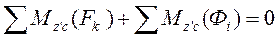
где

Сумма моментов сил 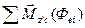по теореме Вариньона равна моменту их равнодействующей, а так как линия действия этой равнодействующей проходит через точку С, то ее момент относительно оси Сz' равен нулю.

Сумма моментов будет равна так же 0, т.к. вектора r и a_n коллинеарные и, соответственно их векторное произведение равно 0.

Последняя сумма моментов равна:

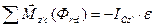
где I_Cz' — момент инерции тела относительно оси Cz'.

ε – угловое ускорение поворота тела относительно центра тяжести.

Таким образом приходим к

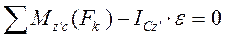
Или

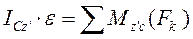
А т.к.

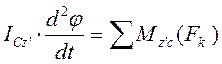
Итак, мы получили три уравнения:

которые представляют собой дифференциальные уравнения плоскопараллельного движения твердого тела. Интегрируя эти дифференциальные уравнения второго порядка, найдем х_с, у_с и φ в функциях от t и, следовательно, найдем движение тела. Если в число сил Fk будут входить неизвестные реакции связей, то для определения движения тела, кроме уравнений, нужно принимать во внимание дополнительные условия, которые данные связи налагают на движение тела.

Date: 2015-09-03; view: 439; Нарушение авторских прав