Динамика материальной точки. Динамика изучает законы движения материальных тел под действием сил

ДИНАМИКА

ОСНОВНОЙ ЗАКОН ДИНАМИКИ ТОЧКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ

Динамика изучает законы движения материальных тел под действием сил. Простейшим материальным объектом является материальная точка. Так называют модель материального тела любой формы, размерами которого в рассматриваемых задачах можно пренебречь и принять тело за геометрическую точку массой, равной массе тела. Более сложные материальные объекты — сплошные тела и механические системы тел — считаются состоящими из материальных точек.

В динамике, в отличие от кинематики, при изучении движения тел учитываются как действующие силы, так и инертность самих материальных тел. Сила характеризует меру механического взаимодействия тел. Инертность же представляет собой свойство материальных тел быстрее или медленнее изменять скорость своего движения под действием приложенных сил. Количественной мерой инертности тела является его Масса.

Все положения динамики получают из ее аксиом, называемых также законами классической механики. Систематически законы динамики были впервые изложены И. Ньютоном.

Первый Закон (закон инерции): изолированная от внешних воздействий материальная точка сохраняет свое состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные силы не заставят ее изменить это состояние. Движение, совершаемое точкой при отсутствии сил, называется движением по инерции.

Это свойство тела называется его инертностью.

Существенным является вопрос о том, по отношению к какой системе отсчета справедлив закон инерции. Ньютон предполагал, что существует некое неподвижное (абсолютное) пространство, по отношению к которому этот закон выполняется. Поэтому в классической механике масса движущегося тела принимается равной массе покоящегося тела, т. е. она рассматривается как постоянная величина, являющаяся мерой инертности тела и его гравитационных свойств.

Теория относительности утверждает, что масса и энергия связаны неразрывно друг с другом. Всякое изменение энергии системы сопровождается изменением его инертной массы. Из этого следует, что с возрастанием скорости движения тела его инертность увеличивается.

Между тем, поскольку закон имеет опытное происхождение должны существовать системы отсчета, в которых с той или иной степенью приближения первый закон будет выполняться. В связи с этим в механике, вводят понятие о инерциальной системой отсчета, в которой справедлив закон инерции.

Второй закон (основной закон динамики) устанавливает, как изменяется скорость точки при действии на нее какой-нибудь силы, а именно: произведение массы материальной точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы.

Математически этот закон выражается векторным равенством

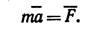
При этом между модулями ускорения и силы имеет место зависимость

Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета. Из этого закона непосредственно видно, что мерой инертности материальной точки является ее масса, поскольку при действии данной силы точка, масса которой больше, т. е. более инертная, получит меньшее ускорение и наоборот.

Если на точку действует одновременно несколько сил, то они, как это следует из закона параллелограмма сил, будут эквивалентны одной силе, т. е. равнодействующей R, равной геометрической сум­ме данных сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид

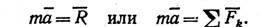
Третий закон (закон равенства действия и противодействия) использовался и в статике. Он устанавливает характер механического взаимодействия между материальными телами. Для двух материальных точек он гласит: две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.

При взаимодействии двух свободных материальных точек, они, согласно третьему и второму законам динамики, будут двигаться с ускорениями, обратно пропорциональными их массам.

Закон независимости действия сил. При одновременном действии на материальную точку нескольких сил ускорение точки в инерциальной системе отсчета от действия каждой отдельной силы не зависит от наличия других приложенных к точке сил, и полное ускорение точки равно векторной сумме ускорений от действия отдельных сил.

Пусть к материальной точке приложена система сил F1, F2,..., Fn, которую мы для краткости будем обозначать также символически через (F). Согласно закону независимости действия сил, ускорение точки от действия каждой из сил системы определится по формуле:

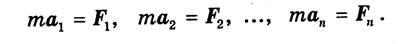
При одновременном действии всех сил системы (F) ускорение точки равно векторной сумме ускорений, вызываемых отдельными силами:

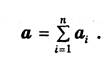
Суммируя равенства получаем основное уравнение динамики точки:

Уравнение остается справедливым и для несвободной материальной точки. В этом случае в число приложенных сил нужно включить также силы реакций связей.

Date: 2015-09-03; view: 610; Нарушение авторских прав