
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Законы Ньютона
|
|
2.1. Ньютоновская механика
Динамика представляет собой раздел механики, исследующий причины движения (силы).
Нерелятивистская классическая механика называется ньютоновской. Термин «нерелятивистская» означает малость характерных скоростей по сравнению со скоростью света в вакууме. Термин «классическая» означает отсутствие квантовых эффектов. Необходимым условием их отсутствия является то, что размер рассматриваемых объектов велик по сравнению с характерным размером атомов.
Ньютоновская механика основана на постулатах, называемых законами Ньютона. Постулаты являются обобщением большого количества опытных фактов.
Первый закон. Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.
Смысл первого закона заключается в постулировании существования инерциальных систем отсчета (ИСО). ИСО связаны между собой преобразованиями Галилея. Если ИСО S' движется относительно ИСО S с постоянной скоростью 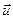 вдоль оси
вдоль оси  , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид
, а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид
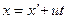 (2.1)
(2.1)
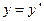 (2.2)
(2.2)
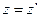 (2.3)
(2.3)
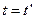 (2.4)
(2.4)
Или, в векторном виде
 (2.5)
(2.5)
Второй закон. В инерциальной системе отсчета изменение импульса материальной точки определяется равнодействующей всех приложенных к ней.
 (2.6)
(2.6)
При постоянной массе системы
 (2.7)
(2.7)
Уравнения (2.1) и (2.2), являясь векторными, представляют собой наборы трех скалярных уравнений.
Третий закон. Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению.
Следствием законов Ньютона является принципиальная возможность полностью описать движение системы материальных точек, зная силы и начальные условия (координаты и скорости всех точек в нулевой момент времени).
2.2. Некоторые силы природы
Сила упругости пружины
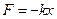 (2.8)
(2.8)
где k – коэффициент жесткости, x – растяжение (сжатие) пружины.
Сила всемирного тяготения
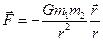 (2.9)
(2.9)
где  - постоянная всемирного тяготения. Знак «минус» соответствует притяжению тел).
- постоянная всемирного тяготения. Знак «минус» соответствует притяжению тел).
Сила тяжести вблизи поверхности Земли
 (2.10)
(2.10)
где  = ускорение свободного падения (MЗ и RЗ – масса и радиус Земли соответственно).
= ускорение свободного падения (MЗ и RЗ – масса и радиус Земли соответственно).
Кулоновская сила (описывает взаимодействие точечных электрических зарядов в вакууме)
 (2.11)
(2.11)
где  - диэлектрическая проницаемость вакуума, q1 и q2 - электрические заряды. Формула (2.11) приведена в системе СИ (при использовании другой системы единиц вместо
- диэлектрическая проницаемость вакуума, q1 и q2 - электрические заряды. Формула (2.11) приведена в системе СИ (при использовании другой системы единиц вместо 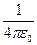 нужно писать другой коэффициент).
нужно писать другой коэффициент).
ЗАДАЧИ
1. На плоскости, образующей угол a с горизонтом, лежит шайба массы m. Какую минимальную силу надо приложить к шайбе в горизонтальном направлении вдоль плоскости, чтобы она сдвинулась? Коэффициент трения m.
Ответ: 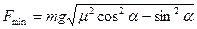 при m > tga; 0 при m < tga
при m > tga; 0 при m < tga
2. Брусок массы m тянут за нить так, что он движется с постоянной скоростью по горизонтальной плоскости с коэффициентом трения m. При каком значении угла наклона a натяжение нити минимально? Чему оно равно?
Ответ:  ,
, 
3. На гладкое проволочное кольцо, расположенное вертикально, надета маленькая бусинка. Кольцо вращается вокруг вертикальной оси, проходящей по диаметру кольца. Где находится бусинка?
Ответ: a - угол с вертикалью,  при g < w2R; a = 0 при g > w2R
при g < w2R; a = 0 при g > w2R
4. Доска массы m2 лежит на гладкой горизонтальной плоскости. На доске находится брусок массы m1, коэффициент трения между доской и бруском равен m. На доску начинает действовать горизонтально направленная сила, зависящая от времени по закону F(t) = at. Найти ускорения тел в зависимости от времени.
Ответ: при 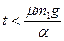
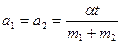 ;
;
при 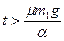
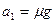 ;
; 
5. Тело начинает скользить с вершины неподвижного клина с основанием L. Коэффициент трения равен m. При каком значении угла a при основании клина время соскальзывания будет наименьшим?
Ответ: m = -2ctga
6. На тело массы m, расположенное на горизонтальной плоскости, действует сила F, направленная вниз под углом a к горизонту. Сила приложена к центру масс, коэффициент трения равен m. Найти ускорение тела.
Ответ: 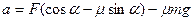 при
при 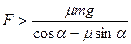 ; 0 при
; 0 при 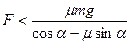
7. На тело массы m в течение времени t действует сила F, направленная горизонтально. Коэффициент трения тела о горизонтальную плоскость равен m. Какой путь пройдет тело до остановки? Начальная скорость тела равна нулю.
Ответ: 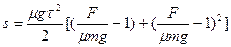 при F > mmg
при F > mmg
8. Подвешенный на нити длины L точечный груз массы m движется в горизонтальной плоскости по окружности. Нить при этом образует угол 60° с вертикалью. Найти скорость движения груза и силу натяжения нити.
Ответ:  ,
, 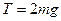
9. На тело массы m, движущееся в вязкой среде, действует сила сопротивления F = -kv2. Начальная скорость тела равна v0. Найти зависимость скорости тела и пройденного пути от времени. x(0) = 0.
Ответ: 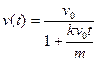 ,
, 
10. Брусок массы m расположен на наклонной плоскости. Коэффициент трения материала бруска о плоскость равен m. Начертить график зависимости силы трения, действующей на брусок, от угла при основании наклонной плоскости.
Ответ: 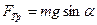 при a < arctg m;
при a < arctg m; 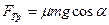 при a > arctg m
при a > arctg m
11. В начальный момент времени тело начинает двигаться с начальной скоростью v 0, вверх по наклонной плоскости с углом у основания a. Через какое время абсолютная величина скорости тела снова станет равной v 0? Коэффициент трения m < tg a.
Ответ: 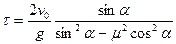
12. Тело соскальзывает без начальной скорости с наклонной плоскости с углом у основания a. Коэффициент трения тела о плоскость изменяется по закону m = bx, где x – координата вдоль плоскости, отсчитываемая от точки начала движения тела. Тело останавливается, не дойдя до основания наклонной плоскости. Найти время движения и путь, пройденный телом.
Ответ: t = p / (bgcosa)1/2; s = 2tga / b
13. На тело массы m, лежащее на гладкой горизонтальной плоскости, в момент времени t = 0 начинает действовать сила F = bt, направленная под углом a к горизонту. Найти скорость тела и пройденный им путь к моменту отрыва от плоскости.
Ответ: 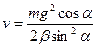 ,
, 
14. На покоившуюся частицу массы m в момент времени t = 0 начинает действовать сила F = A t(t-t), где A – постоянный вектор, t - время, в течение которого действует данная сила. Найти путь, пройденный частицей за время действия силы.
Ответ:  ,
, 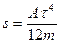
15. Тело массы m, летящее со скоростью v0, тормозится силой, зависящей от времени по закону 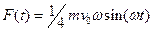 , где
, где 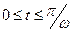 . Чему будет равна скорость тела после окончания действия силы?
. Чему будет равна скорость тела после окончания действия силы?
Ответ: 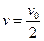
16. По наклонной плоскости скользят два тела одинаковой массы, связанные невесомой нерастяжимой нитью. Сила натяжения нити равна T. Трения между одним телом и плоскостью нет. Определить силу трения между доской и другим телом.
Ответ: Fтр = 2T
17.
 |
Найти ускорения тел системы, изображенной на рисунке. Блок и нити невесомы, нить нерастяжима.
Ответ: 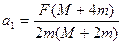 ,
,  ,
, 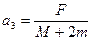
18.
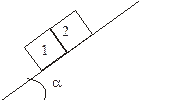 |
На наклонную плоскость, составляющую угол a с горизонтом, поместили два соприкасающихся бруска 1 и 2. Массы брусков m1 и m2, коэффициенты трения соответственно m1 и m2, причем m1 > m2. Найти силу взаимодействия между брусками в процессе движения.
Ответ: 
19. По деревянным сходням, образующим угол a с горизонтом, втаскивают за привязанную к нему веревку ящик. Коэффициент трения ящика о сходни m. Под каким углом к горизонту следует тянуть веревку, чтобы с наименьшим усилием втащить ящик?
Ответ: 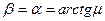
- В сферическую полость поместили гантель, представляющую собой два шарика массы m каждый, соединенные невесомым жестким стержнем. Определить силу давления шариков на стенки сразу после того, как гантель отпустили. Радиус шариков много меньше радиуса полости.
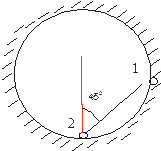
Ответ: 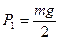 ,
, 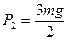
21. В системе массы тел равны M, m1 и m2. Трения нет, массы блоков и нитей пренебрежимо малы. Найти ускорение тела m1. Исследовать возможные случаи.
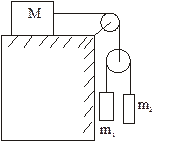 |
Ответ: 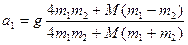 , при m1 = m2 = m
, при m1 = m2 = m 
-

В системе, изображенной на рисунке, массы тел равны m1 и m2, нити невесомы и нерастяжимы. Найти ускорения тел и силу натяжения нити.
Ответ:  ,
, 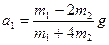 ,
, 
23.
 |
Шарик массы m имеет отверстие и может скользить по невесомой нерастяжимой нити с некоторым трением. В начальный момент времени шарик находился напротив нижнего конца стержня, имеющего массу M и длину L (см. рисунок). После того как систему предоставили самой себе, оба тела начали двигаться с постоянным ускорением. Найти силу трения между шариком и нитью, если через t секунд после начала движения шарик оказался напротив верхнего конца стержня.
Ответ: 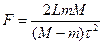
24. По наклонной плоскости скользят два тела одинаковой массы, связанные невесомой нерастяжимой нитью. Сила натяжения нити равна T. Трения между одним телом и плоскостью нет. Определить силу трения между доской и другим телом.
Ответ: Ответ: 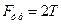
25. 
Найти ускорение a тела 2, если его масса в h раз больше массы бруска 1 и угол между наклонной плоскостью и горизонтом равен a. Трением пренебречь.
Ответ: 
- В начальный момент времени тело начинает двигаться с начальной скоростью v 0 вверх по наклонной плоскости с углом у основания a. Через какое время абсолютная величина скорости тела снова станет равной v 0? Коэффициент трения m < tg a.
Ответ: 
- По внутренней абсолютно гладкой поверхности конуса вращается небольшое тело. Чему равна его скорость, если окружность находится на высоте h от вершины конуса?
Ответ: 
-
 В системе массы тел равны M и m. Коэффициент трения между телом и плоскостью равен m. Какую минимальную силу надо приложить, чтобы сдвинуть систему с места? Трения между телами нет.
В системе массы тел равны M и m. Коэффициент трения между телом и плоскостью равен m. Какую минимальную силу надо приложить, чтобы сдвинуть систему с места? Трения между телами нет.
Ответ: 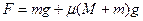
29. На неподвижный клин с углом у основания a на высоте H положили и отпустили небольшое тело. Найти время, за которое тело опустится на высоту H/2. Трением пренебречь.
Ответ: 
- На горизонтальной плоскости лежит клин массы M с углом у основания a. На клин помещен брусок массы m. Коэффициент трения между бруском и поверхностью клина ра
 вен m. С какой горизонтальной силой F надо действовать на вертикальную поверхность клина, чтобы брусок не скользил по клину? Соотношение между a и m такое, что при F = 0 брусок скользит по клину. Трение между клином и горизонтальной плоскостью отсутствует.
вен m. С какой горизонтальной силой F надо действовать на вертикальную поверхность клина, чтобы брусок не скользил по клину? Соотношение между a и m такое, что при F = 0 брусок скользит по клину. Трение между клином и горизонтальной плоскостью отсутствует.
Ответ: 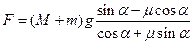
- По наклонной плоскости с углом наклона α1 к горизонту с высоты H1 без начальной скорости соскальзывает тело. Достигнув нижней точки, оно начинает подниматься верх по наклонной плоскости с углом наклона a2. Полагая коэффициенты трения тела о плоскости равными m1 и m2 соответственно, найти высоту подъема тела. Переход с плоскости на плоскость плавный, короткий и гладкий.
Ответ: 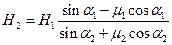
- Две точечные массы m1 и m2 соединены невесомой нерастяжимой нитью, продетой сквозь кольцо массы m3. Массы m1 и m2 лежат рядом на горизонтальном столе, а кольцо висит на
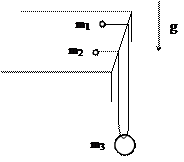 нити, спускающейся через край стола. Нити подходят к краю стола перпендикулярно. Трение отсутствует. Найти ускорение кольца.
нити, спускающейся через край стола. Нити подходят к краю стола перпендикулярно. Трение отсутствует. Найти ускорение кольца.
Ответ: 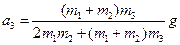
- Невесомый блок подвешен к потолку. Через блок перекинута невесомая нерастяжимая нить. К концам нити прикреплены грузы массами m1 и m2. Найти силу, с которой блок действует на потолок, когда грузы движутся свободно в поле тяжести g.
Ответ: 
- По стене ползут вверх два одинаковых кирпича. На нижний кирпич действует сила F, направленная под углом a к вертикали. Коэффициент трения материалов кирпичей о материал стены равен m. Найти силу давления верхнего кирпича на нижний.
Ответ: 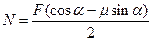
- Тело массы m находится на плоской поверхности. Коэффициент трения между телом и поверхностью равен m. На тело в течение времени τ действует горизонтальная сила, зависящая от времени по закону
 . Найти зависимость силы трения от времени Fтр(t) и нарисовать график этой зависимости для 0 £ t £ 2τ.
. Найти зависимость силы трения от времени Fтр(t) и нарисовать график этой зависимости для 0 £ t £ 2τ.
Ответ: 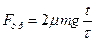 при
при  и
и 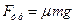 при
при 
- На абсолютно гладком столе лежит доска массы M. На доске лежит грузик массы m. Коэффициент трения между грузиком и доской равен m. С какой минимальной горизонтальной силой надо тянуть за доску, чтобы она выскользнула из-под грузика?
Ответ: 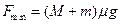
Date: 2015-09-03; view: 3386; Нарушение авторских прав