Ющей на отрезке

Теорема 1.

Функция, непрерывная на отрезке [ a,b ] и имеющая неотрицательную (положительную) производную на интервале (a,b), не убывает (строго возрастает) на [ a,b ].

Доказательство.

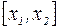Пусть Тогда на отрезке выполняется условие теоремы Лагранжа. Поэтому на интервале 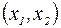найдется точка с, для которой

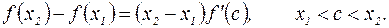
По условию 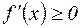, т.е. 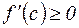на (a,b), поэтому т.е. функция не убывает.

Если же 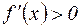на (a,b), то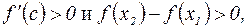 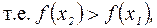функция строго возрастает.

Поскольку 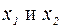– произвольные точки отрезка [ a,b ], то теорема справедлива для всего отрезка [ a,b ].

Теорема 2.

Если функция имеет на интервале (a,b) производную, равную нулю, то она постоянна на (a,b).

Теорема о знаках производной слева и справа от точки экстремума

Теорема 3.

Если функция f непрерывна в окрестности точки 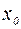и имеет производную

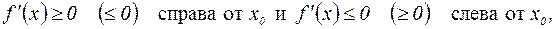
то 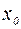– точка локального минимума (максимума) функции f.

Доказательство.

Следует из формулы конечных приращений Лагранжа:

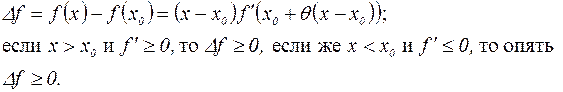
Таким образом, функция имеет локальный минимум. Доказательство для случая локального максимума аналогично.

Теорема 4.

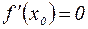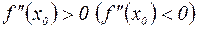Если функция f удовлетворяет условиям и , то 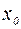есть точка локального минимума (максимума) функции f.

Доказательство.

Если существует вторая производная 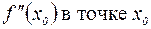, то в окрестности этой точки существует и непрерывна первая производная 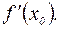Если 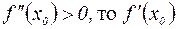возрастает в точке .

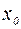Поскольку по условию 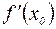=0, то это означает, что справа от 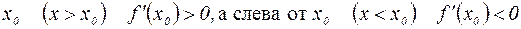. Тогда в соответствии с теоремой 3 функция имеет в точке 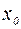минимум. Аналогичное рассуждение можно провести для случая, когда 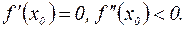Теорема доказана.

Date: 2015-09-02; view: 385; Нарушение авторских прав